ACT Math: Preparing for Higher Math: Functions

Welcome back to another Fiveable guide for ACT Math!🎉 This guide will specifically cover the Functions section of ACT Math, which will make up 12-15% of the math questions, or about 7-9 questions out of 60. 

You will be asked to demonstrate your knowledge of several different types of functions, including linear, radical, piecewise, polynomial, exponential, and logarithmic, from their definitions and notations to their representations and applications, as well as their graphs. 

Let’s break down the skills you need to be successful in this topic and walk through some practice questions together. Remember, you got this!!

---

🤓 Functions Subtopics

ACT lists certain skills that may be tested under the Functions section. We’ve divided them into subtopics for easier and more comprehensive learning. 

🔢 Definitions, Notations, and Applications of Function 

This subcategory is all about understanding functions algebraically. You will be asked to calculate the values of functions, which may involve manipulating the function’s algebraic form. Sometimes you may need to interpret what a value, variable, or characteristic of a function represents in a given situation or even define a function based on a provided scenario. 

 📈 Representing Functions as Graphs

This subtopic is about representing functions visually on a coordinate plane. You will be tested on your ability to graph different types of functions and you ability to interpret them. Also be prepared to manipulate graphs themselves, such as translating them, and understand how these different manipulations affect the algebraic form of a function. 

---

🔢 Definitions, Notations, and Applications of Function 

🧠 What You Need to Know

You will need to…

• • Know what a function is!- - A function describes a relationship between a set of inputs and a set of outputs, where each input is related to exactly one output.
• • Know the basics of different kinds of functions- - Including, but not limited to, linear, radical, piecewise, polynomial, exponential, and logarithmic function- - Check out the Functions section this Fiveable Guide for more review: ACT Math: Algebra & Functions You will also need to know how to…
• • Calculate the (input or output) value of a function.- - Evaluate a function in its algebraic form; calculate the output value of a function given an input value.- - Replace the input variable of the function with the given value.- - Compute the result. This is the output value. You should only end up with one value as an input may only have one output according to the definition of a function.- - Note: This process may involve manipulating the equation to isolate the output variable on one side.- - Solve a function in its algebraic form; calculate the input value of a function given an output value.- - Set the given output equal to the function’s formula.- - Solve for the input. You may end up with multiple values as many inputs can have the same output.- - Note: This process likely involves manipulating the equation to isolate the input variable on one side.
• • Interpret a function in the context of the question.- - What does an input value mean in the given context? An output value? A y-intercept? A slope? …
• • Formulate a function based on a relationship detailed in the problem statement.- - How can we write a function that describes the written scenario mathematically?

🤓 Applying Your Knowledge

Interpreting and Evaluating Functions Practice

The number of fish, f, in Skipper’s Pond at the beginning of each year can be modeled by the equation f(x) = 3(2^x), where x represents the number of years after the beginning of the year 2000. For example, x = 0 represents the beginning of the year 2000, x = 1 represents the beginning of the year 2001, and so forth. According to the model, how many fish were in Skipper’s Pond at the beginning of the year 2006?

A) 96

B) 192

C) 384

D) 1,458

E) 46,656

Credits: ACT, Inc - Question 7 from Preparing for the ACT Test Guide | 2023-2024

The answer is B) 192. 

This problem mainly tests our ability to evaluate a function, while also gauging our understanding of functions in real-world contexts. Let’s first recall the steps for evaluating functions listed above! 🧠

Yes, that’s right! We want to replace the input variable of the function with the given input value and then compute the result.

So, what is our given input value?

Well, this problem doesn’t really give that to us outright. In the question it asks “how many fish were in Skipper’s Pond at the beginning of the year 2006?” Does that mean that x = 2006? NO! 

The problem tells us that for this model, x = the number of years after the beginning of the year 2000 = given year - 2000. Thus, x = 2006 - 2000 = 6 for our purposes. Now, we just need to plug x = 6 into f(x) = 3(2^x), the given function. 

f(6) = 3(2^6)

       = 3 * 64

       = 192

So f(6) or the number of fish in Skipper’s Pond at the beginning of the year 2006 is B) 192!

Formulating Functions Practice

If a publisher charges $15 for the first copy of a book that is ordered and$12 for each additional copy, which of the following expressions represents the cost of y books?

F) 12y + 3

G) 12y + 15

H) 15y - 3

J) 15y + 3

K) 15y + 12

Credits: ACT, Inc - Question 60 from Preparing for the ACT Test Guide | 2023-2024

The answer is F) 12y + 3. 

This problem mainly tests our ability to model a situation using a function. So, how exactly do we go about that?

Well, we are asked by the problem to write an expression that models the cost of y books. 📚Do each of the y books cost the same?

No! The publisher charges $15 for the first copy, but the rest of the y books cost$12 each. This means that the cost of the first of the y books can be modeled by “15 *1” or “15”, and the cost of the other y books can be modelled by “12(y-1)”. Be careful to note that it isn’t “12y” as y is the TOTAL number of books, not the number of books IN ADDITION to the first one. 

Adding the two components, “15” and “12(y-1)” together, we get 15 + 12(y-1) as the model for the total cost of y books. Simplifying, we get:

15 + 12y - 12

12y + 3 or A). 

---

📈 Representing Functions as Graphs 

🧠 What You Need to Know

You will need to know how to…

• • Graph different kinds of functions- - Here are some tips and tricks!- - Familiarize yourself with the shapes of the graphs of different functions- - Plug in values and plot a few points- - If you have a graphing calculator, use it!!!
• • Determine an equation from a graph of a function- - Same tips from above apply!
• • Manipulate graphs- - What does it mean to transform a graph?- - If this graph is manipulated in such and such way, how does that affect the algebraic form of the function?

🤓 Applying Your Knowledge

Manipulating Graphs Practice

Credits: ACT, Inc - Question 58 from Preparing for the ACT Test Guide | 2023-2024

The answer is K) 3 cos(2x). 

This problem tests our ability to determine an equation from a graph and to manipulate graphs. So how exactly should we approach this problem?

Well, let's begin by picturing the most basic cosine function, cos(x). What does it look like? 

Image Courtesy of Study.com

It’s amplitude is 1 and it’s period is 2π. But what is the amplitude and period of our function? The graph of our function manipulates the graph of cos(x) so that it has an amplitude of 3 and a period of π. 

How do these transformations affect the algebraic form of the function? Well, multiplying cos(x) by A, where A is a constant, changes the function’s amplitude to be A. So, 3cos(x) has an amplitude of 3. Furthermore, to change the period of a cosine function, we can multiply x by B, another constant, such that cos(Bx) has a period of 2pi/|B|. For example, cos(2x) has a period of π.

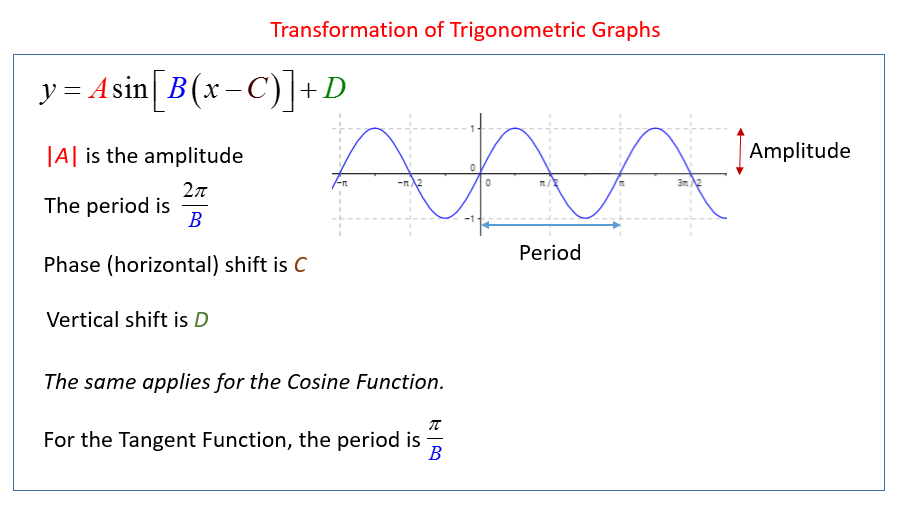
Image Courtesy of Onlinemathlearning.com

Combining these bits of knowledge together, the equation for a cosine function with an amplitude of 3 and a period of π is 3cos(2x). 

Remember, when in doubt, we can always plug in values to the answer choices to plot them and see if they match the given graph. Or use your graphing calculator!

---

Conclusion

Congratulations!🎊 You’ve made it to the end of ACT Math: Preparing for Higher Math: Functions. Hopefully you have a better understanding of functions and how to approach these kinds of problems on the ACT. 

Good luck studying for the ACT, we believe in you! 👏

Need more ACT resources? Check out our other ACT Math Guides with practice problems. Keep up the good work 🥳!!

**tldr; The ACT Math section is an hour-long test consisting of 60 questions. Calculators are allowed on the whole test! A major content area for this section is Functions, which consists of around 7-9 questions. For this category, you should be able to understand functions both algebraically and graphically. **