<< Hide Menu
2.1 Defining Average and Instantaneous Rates of Change at a Point
2 min read•june 18, 2024
Welcome back to AP Calculus with Fiveable! After covering Limits and Continuity in Unit 1, we are now diving into Unit 2: Differentiation - Definition and Basic Derivative Rules. Our focus in this section is to understand the concepts of average and instantaneous rates of change at a point. Let’s get into it! ⬇️
✈️ Average Rate of Change
In real-world scenarios, the average rate of change is often used to represent average speed, average velocity, or average growth rate. In calculus, understanding rates of change is crucial, which is much like the concept of slope in algebra.
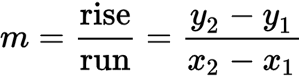
Image courtesy of Rebecca
For any two points on a continuous function within the interval , the average rate of change can be expressed as:
This is also the slope of the secant line between any two points.
⛷️ Instantaneous Rate of Change
While the average rate of change informs us how a function behaves over an interval , the instantaneous rate of change tells us the rate of change at an exact point. In calculus, we express this using the derivative.
The instantaneous rate of change of a function at a specific point is denoted as and is given by the limit:
This limit represents the slope of the tangent line to the graph of at the point . In other words, it tells us how fast the function is changing precisely at the point .
🏋️♂️**** Practice Problems
Let’s work on a few questions to get the concepts down! Here are a few steps you can follow when approaching problems that ask you to solve for average rate of change or instantaneous rate of change:
- 👀 Identify the function and the interval.
- ✏️ Apply the formula for the rate of change you are solving for, either average or instantaneous.
- ✅ Substitute the values and solve.
1) Solving Average Rate of Change
Consider the function over the interval . Calculate the average rate of change.
👉 Step 1: Identify the function and the interval.
👉 Step 2: Apply the formula for an average rate of change.
Average rate of change
👉 Step 3: Substitute the values and solve.
Average rate of change
2) Solving Instantaneous Rate of Change
Consider the function . Find the instantaneous rate of change at .
👉 Step 1: Identify the function and the point.
👉 Step 2: Apply the formula for the instantaneous rate of change.
Instantaneous rate of change:
👉 Step 3: Substitute the values and solve.
Instantaneous rate of change:
😌 Summing it Up
You made it to the end of the first topic in unit 2! Great work. Here’s a quick table displaying the differences between average and instantaneous rates of change for you to take with you throughout the unit.
| Aspect | Average Rate of Change | Instantaneous Rate of Change |
| Time Span | Over an interval of values | At a specific instant |
| Measurement | Represents an average behavior | Represents the exact rate at one point on a function curve |
| Calculation | Uses a slope formula between two points on a function curve | Utilizes the derivative formula for a specific point |
| Precision | Gives an approximation | Provides an exact value |
| Purpose | Useful for understanding overall trends or changes | Helpful for determining precise moments of change |
Best of luck! 🍀

© 2024 Fiveable Inc. All rights reserved.