2.4 Connecting Differentiability and Continuity: Determining When Derivatives Do and Do Not Exist

2.4 Connecting Differentiability and Continuity: Determining When Derivatives Do and Do Not Exist

Welcome back to AP Calculus with Fiveable! This topic focuses on determining when a derivative exists and relating it to the concept of continuity. Let's combine our skills in determining continuity over an interval with the knowledge of derivatives and rates of change to continue building our derivative skills. 🧱

↗️ Continuity and Differentiability

Most of the curves you encounter in AP Calculus will be both continuous and differentiable. But we can run into problems if it turns out that it doesn't fit both conditions! Brush up on the rules for continuity with this guide: Confirming Continuity over an Interval.

For a curve to be differentiable, it must have a derivative at every point in its domain. This means that if you zoom in very close, the graph will be smooth and look like a straight line. This line does not have to be only horizontal! ↗️

Take a look at this graph of $\cos(x)$, and notice that as we zoom into the point $(0,1)$, the curve looks like a line.

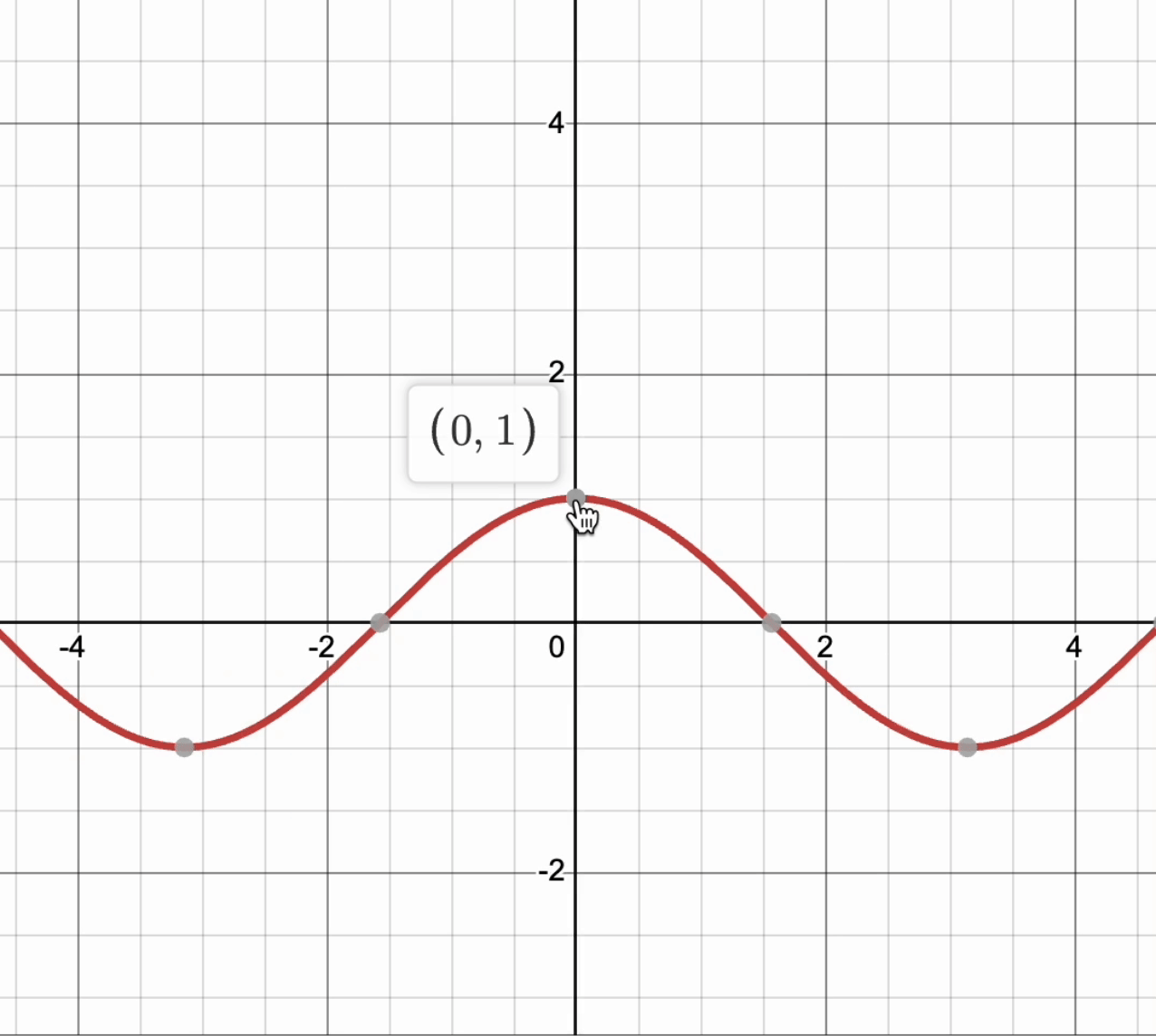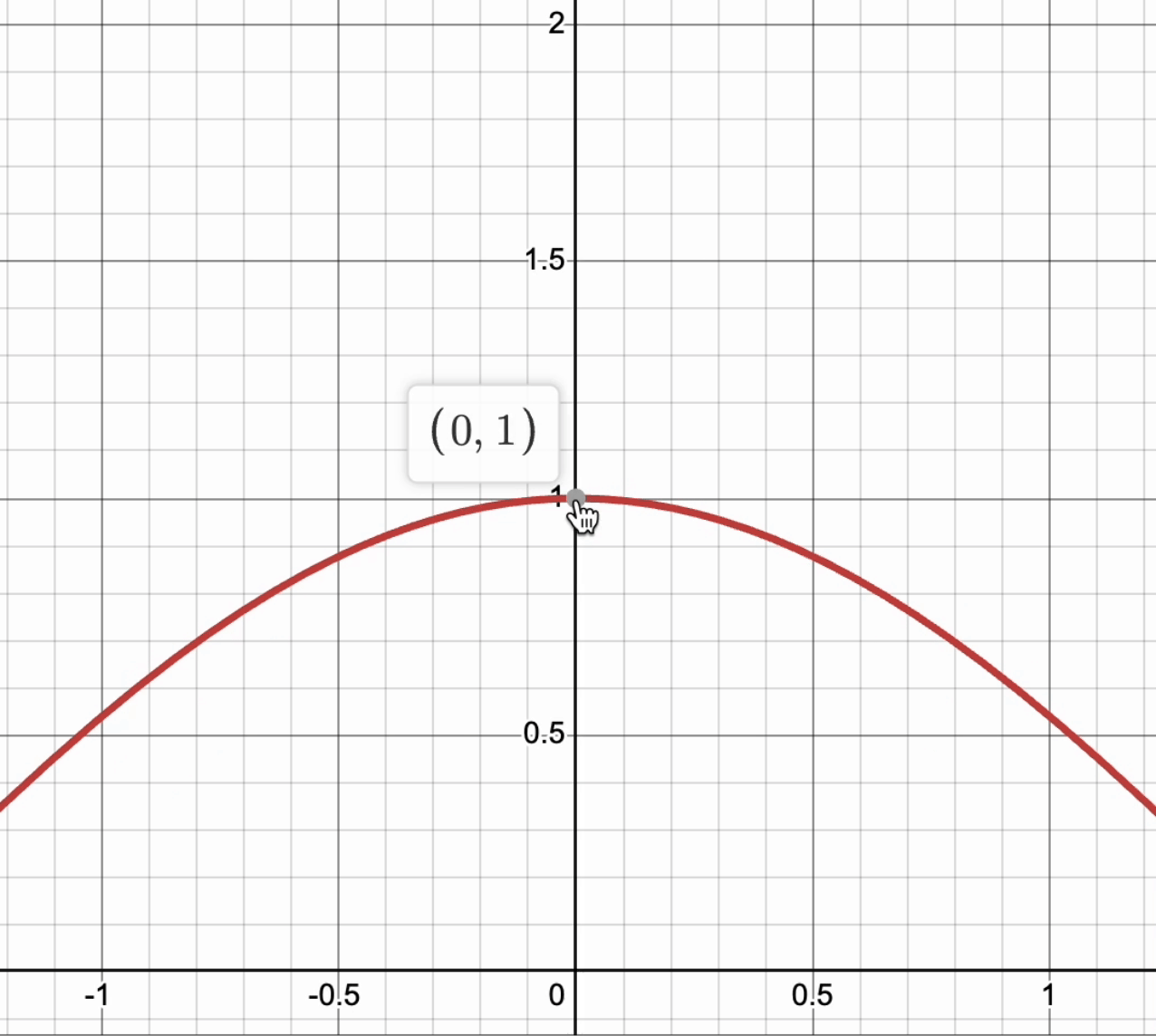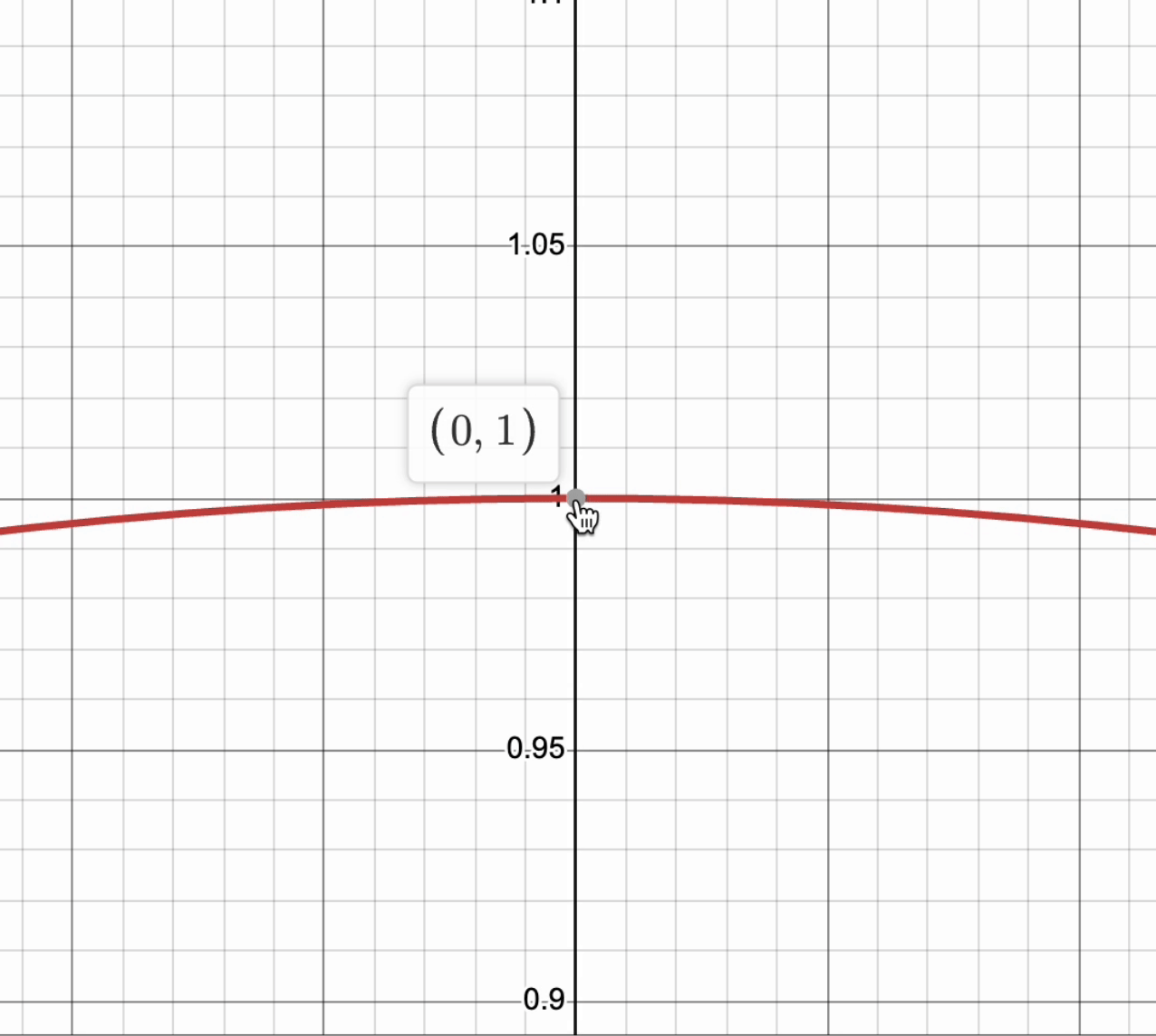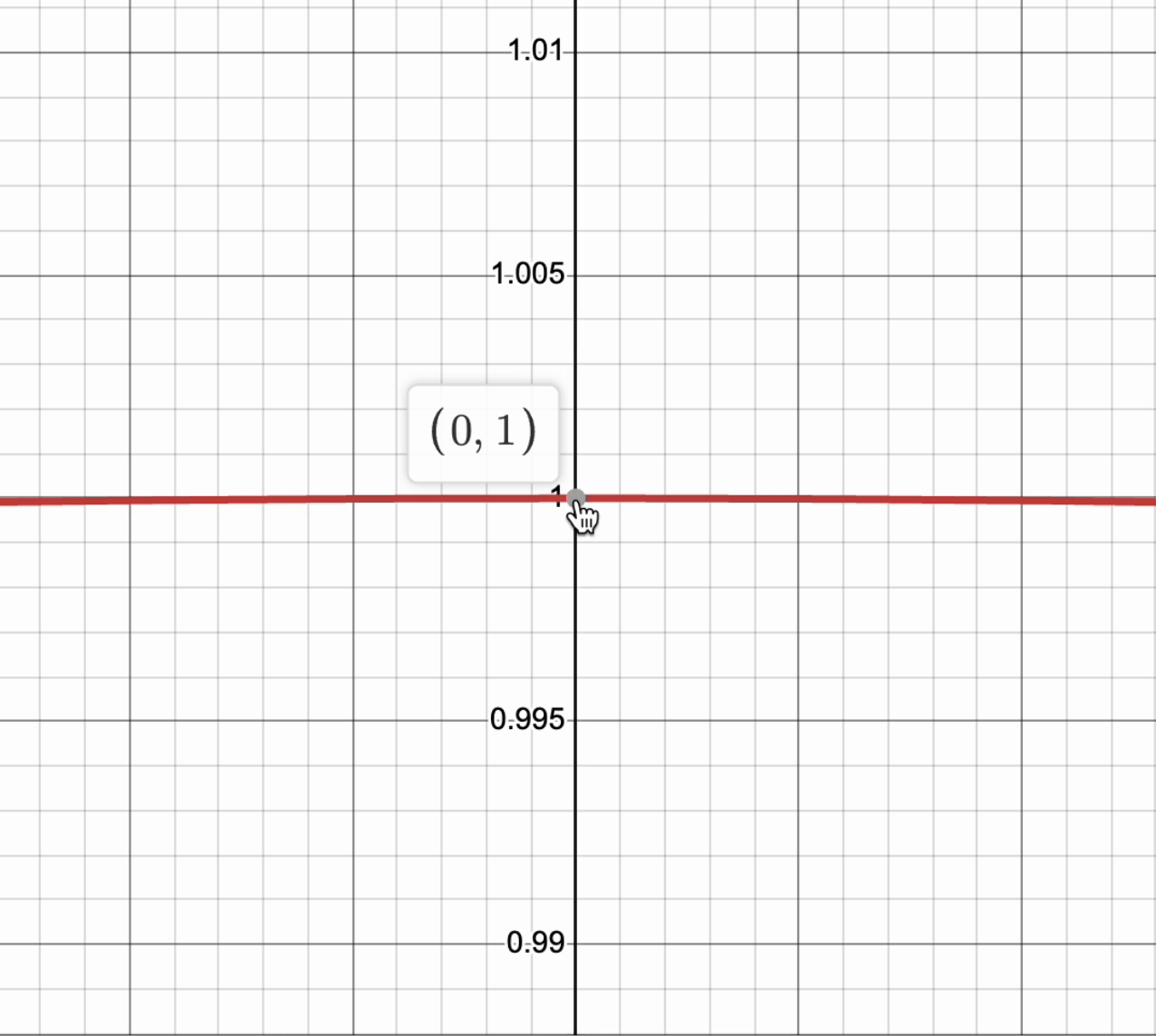
Graph created with Desmos

For a curve to be differentiable at a single point, the right-hand limit of the derivative must equal the left-hand derivative, as well as the derivative at that point.

If a curve is differentiable, it must also be continuous. However, if a curve is continuous, it does not have to be differentiable! A curve is not differentiable if: it is discontinuous, has a sharp shift in the rate of change, or contains a vertical tangent.

Let’s check out these scenarios and observe why the curve is not differentiable at these points.

🕳 Discontinuous Graphs

Unequal Derivatives

For most discontinuous graphs, we can see that the derivatives approaching the point from either side will not be equal.

For example, $g(x) = \frac 1{x+2}$ looks like the following in the graph below. Since the denominator cannot equal 0, $x \neq 2$. The domain of this graph is $(-∞,-2) \cup (-2,∞).$

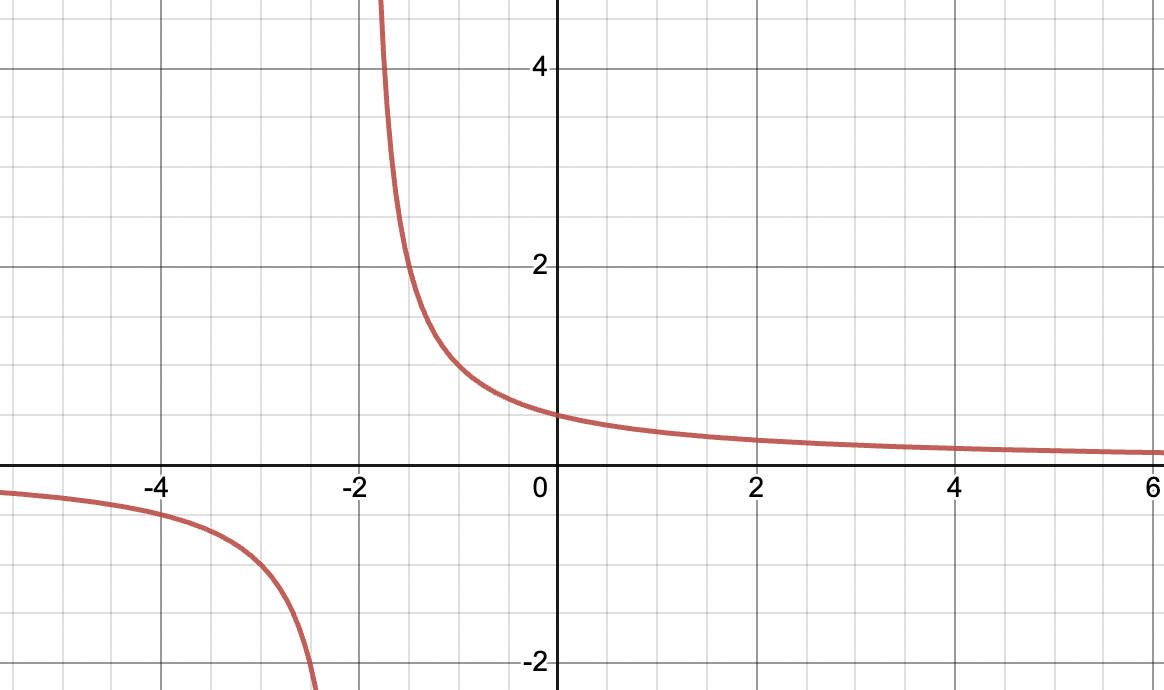
Graph created with Desmos

We also see that $lim_{x\to -2^{-}} g'(x) <0$, while $lim_{x\to -2^{-}} g'(x) >0$. Hence, we can conclude that this graph is not continuous, and therefore not differentiable at $x = -2$.

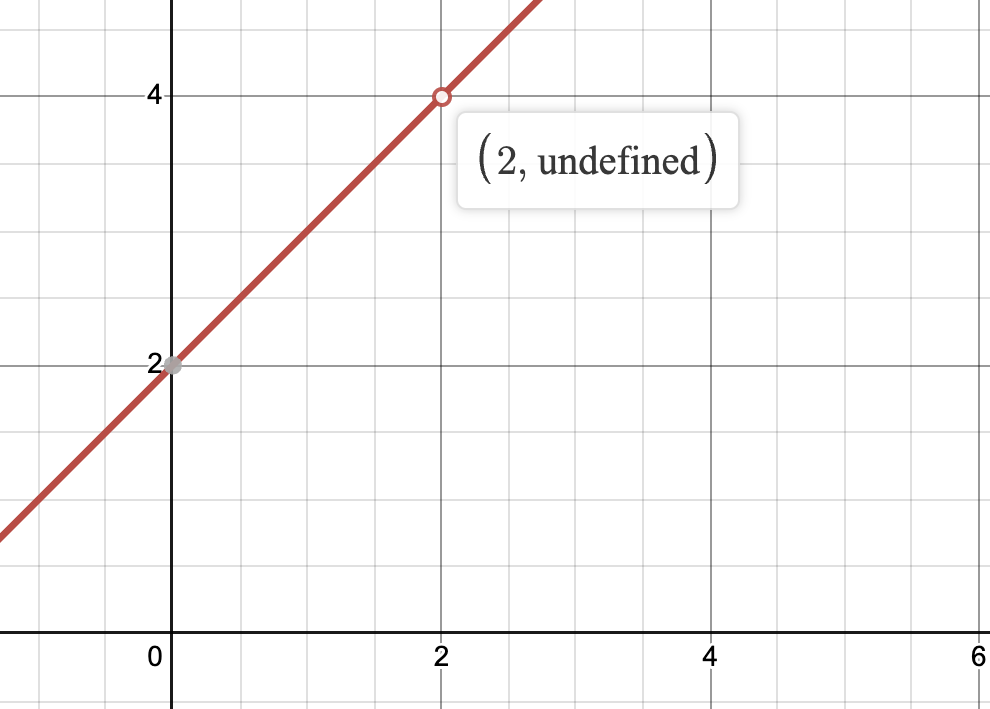
Jump Discontinuity

We can apply the same logic to a graph with a jump discontinuity, such as the following graph. This graph is also discontinuous because $lim_{x\to 2^{-}} f'(x) >0$ while $lim_{x\to 2^{-}} f'(x) <0$.

Graph created with Desmos

Removable Discontinuity

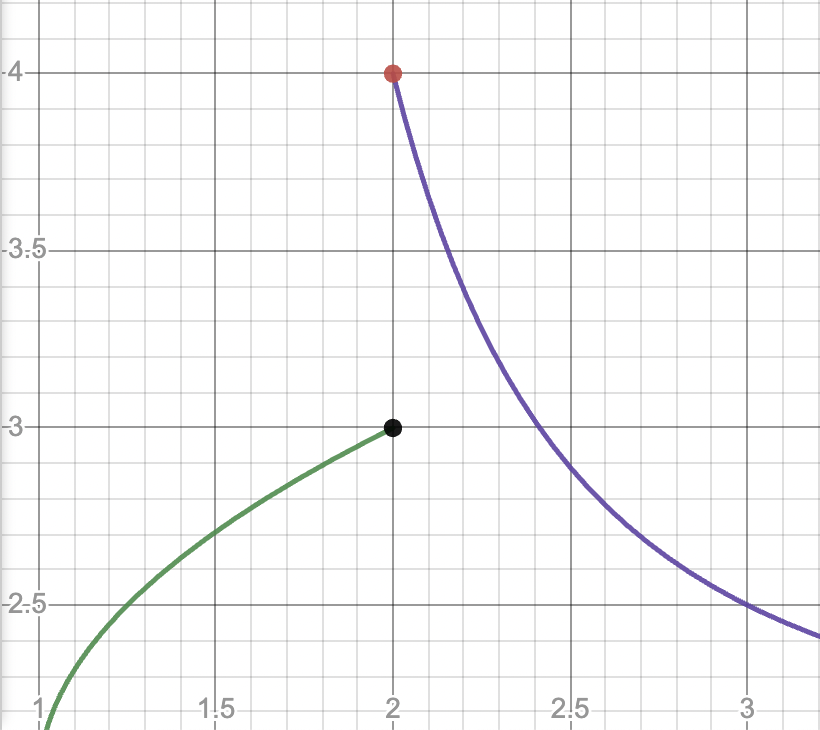
For a removable discontinuity, we have to take it a step further. Take a look at the graph of $h(x) = \frac{x^2-4}{x-2}$ below. We can see that there is a removable discontinuity at $x = 2$.

Graph created with Desmos

We can determine, by hand or with a calculator, that the derivative is equal to $1$ at all points except for $x = 2$ . But what about at $x = 2$? The calculator will tell us that the derivative is undefined, or does not exist. Since $lim_{x\to2^{-}} h'(x) = lim_{x\to 2^{+}} h'(x)$ but $\neq f'(2)$, we determine that the function is not differentiable at $x = 2$.

Therefore, if the curve is discontinuous at a point, it cannot be differentiable.

⬆️ Vertical Tangents

Take a look at the graph of $f(x)=2\left(x+2\right)^{\left(\frac{1}{3}\right)}$ below.

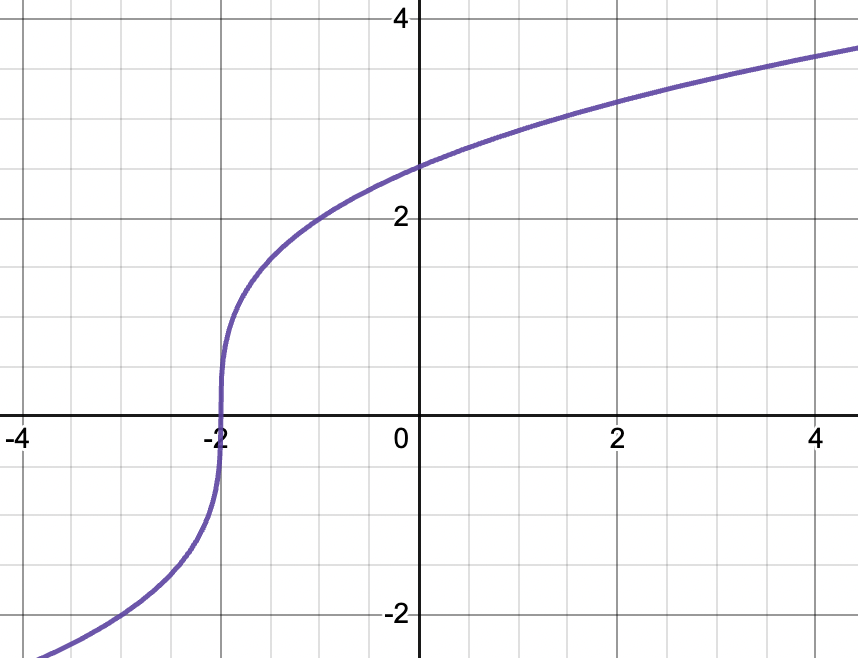
Graph created with Desmos

What would the derivative at $x = -2$ be equal to? If we think about the slope of a line tangent to $f(x)$ at $x = -2$, the slope would be $∞$ because the change in $y$ values would be a number divided by the change in $x$ values: $0$. Therefore, the derivative at $x = -2$ does not exist, and makes the curve not differentiable at $x = -2$.

📐 Corners and Cusps

We can determine that a curve will not be differentiable at a corner or a cusp because the derivative will not approach the same value on both sides of the point. Additionally, there may be a vertical tangent! Let's observe the graphs below.

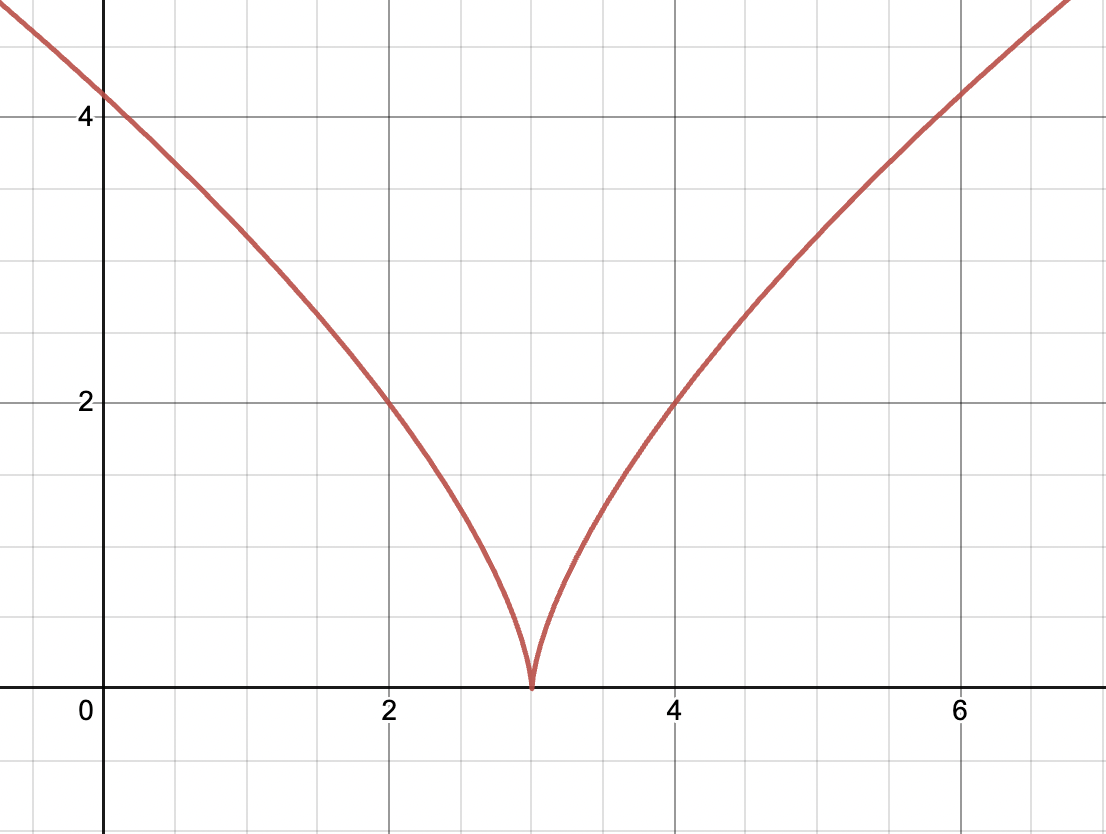
This is the graph of $f(x) =2\left(x+2\right)^{\left(\frac{1}{3}\right)}$. We can see that this graph would have a vertical tangent line as we approach $x = 3$, so it cannot be differentiable.

Graph created with Desmos

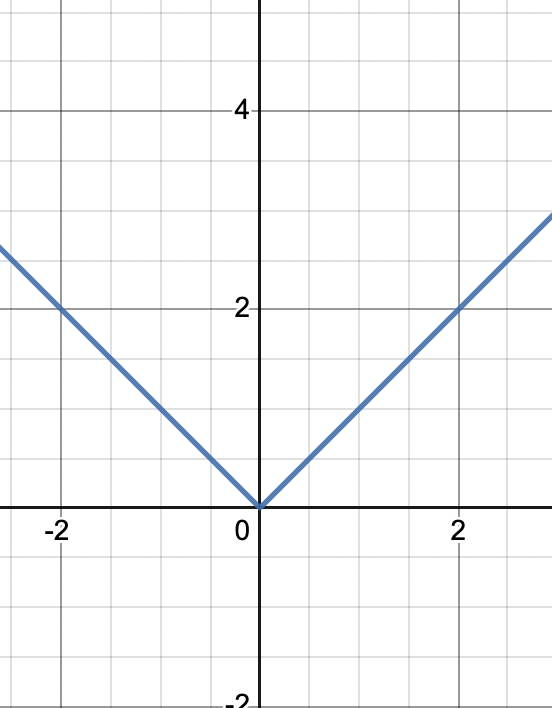
Let’s look at another graph! This is the graph of $g(x) = |x|$. This function has a corner, and is not diffferentiable because $lim_{x\to 0^{-}} g'(x) <0$ while $lim_{x\to 0^{-}} g'(x) >0$, and cannot be equal.

Graph created with Desmos

Nice work! Now you can identify when the curve is differentiable at a point. 🙌

---

🧮 Practice Problems

Let’s work on a few questions and make sure we have the concept down!

1) Graphically Identifying Differentiability at a Point

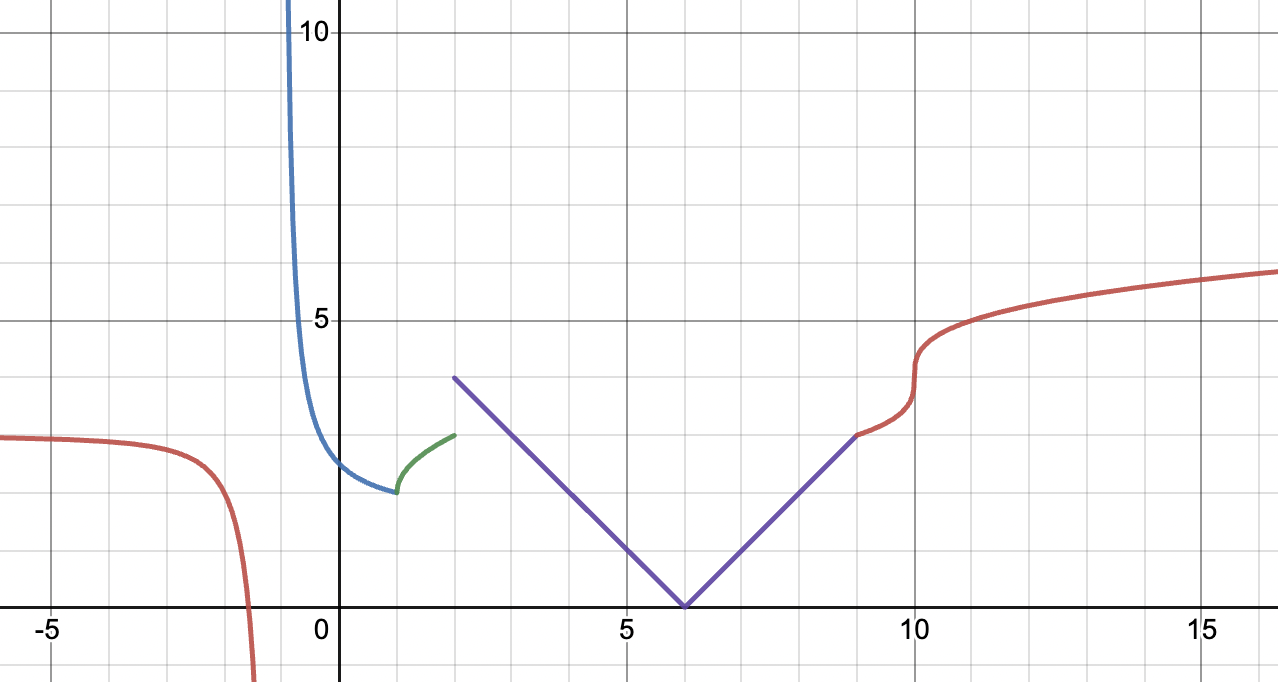
Identify the number of points where the piecewise function $f(x)$ is not differentiable.

Graph created with Desmos

The correct answer here is $6$! Let’s list them out: ⬇️

1. There is an infinite discontinuity at $x = -1$.
2. There is a jump discontinuity at $x = 2$.
3. There is a cusp at $(1,2)$.
4. There is a second cusp at $(9,3)$.
5. There is a corner at $(6,0)$ .
6. Finally, we have a vertical tangent at $(10,4)$!

That was excellent work. Let’s try to determine differentiability with an algebraic method.

2) Determining Differentiability at a Point

The following free-response question (FRQ) is from the 2003 AP Calculus AB examination administered by College Board. All credit to College Board.

The function $f(x)$ can be represented by the following piecewise function:

Given that $f(x)$ is continuous at $x = 3$, is the function differentiable?

To solve this question, we need to check if the derivative approaches the same value from both sides of the function. Let’s get started!

👉 Checking the Left-hand Side

To check the derivative on the left-hand side, we need to take the derivative of the equation representing the function when $x < 3$.

$f'(x) = \frac{d}{dx}\left(\frac{8}{5}\sqrt{x+1}\right) = \frac{4}{5\sqrt{x+1}}$

Therefore, $lim_{x\to 3^{-}} f'(x) = \frac{4}{5\sqrt{3+1}}= \frac{4}{5(2)} = \frac{2}{5}$. Nice work!

👉 Checking the Right-hand Side

To check the derivative on the right-hand side, we need to take the derivative of the equation representing the function when $x \geq 3$.

$f'(x) = \frac{d}{dx}\left(\frac{2}{5}x + 2\right) = \frac{2}{5}$

Therefore, $lim_{x\to 3^{+}} f'(x) = \frac{2}{5}$. Almost there…

👆 Checking $f'(x)$ exists at $x = 3$

To check the derivative at the point, we need to take the derivative of the equation representing the function when $x = 3$, which is the same as when $x \geq 3$.

Therefore, $lim_{x\to 3^{-}} f'(x) = \frac{2}{5}$.

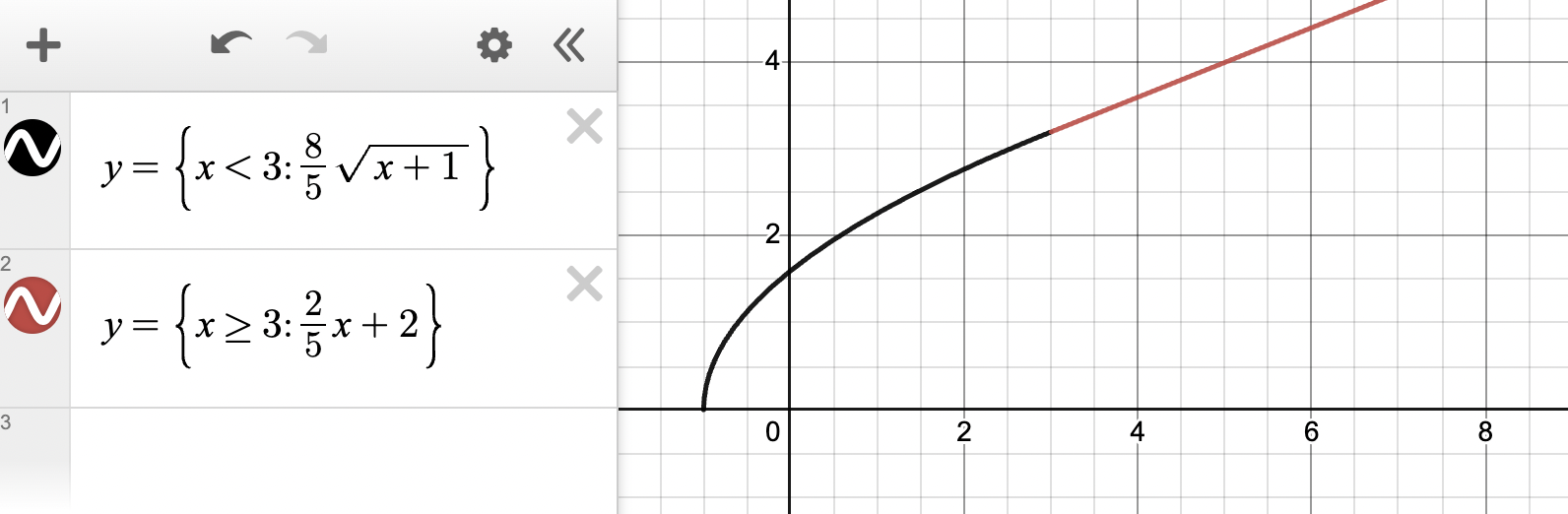
Now we check that all of the limits equal each other, and find that the function $f(x)$ is differentiable at $x = 3$! Check the graph below to confirm our work.

Graph created with Desmos

As we can see from the graph, the function $f(x)$ is smooth at $x = 3$, and is therefore differentiable. Amazing work! 👏

---

🌟 Closing

Great job! 🚀👩‍🚀

You're mastering these concepts, and with practice, you'll navigate derivatives and continuity with confidence. Determining when derivatives exist and ensuring continuity is a crucial skill in AP Calculus. As you encounter questions on the exam, remember to check for domain restrictions and assess piecewise continuity.

Image Courtesy of Giphy