2.8 The Product Rule

2.8 The Product Rule

Welcome back to AP Calculus with Fiveable! This topic focuses on taking the derivative of a product. We’ve worked through derivatives at a point, sum and difference rules, and trigonometric derivatives, so let's keep building our derivative skills. 🙌

🏁 Product Rule Definition

To find the derivative of a product of functions, we need to multiply the first function by the derivative of the second and add it to the second function multiplied by the derivative of the first.

A fun way to remember this rule is by saying:

“First d second (first function times the derivative of the second)

Plus second d first (second function times the derivative of the first).” 😁

This is necessary because the product of derivatives of two functions does not equal the derivative of a product of two functions.

✏️ Product Rule: Walkthrough

For example, let’s find the derivative of the following function:

Using the product rule, we can find that:

If we incorrectly attempt to calculate the derivative of $f(x)$, it would say

However, $\textcolor{green}{sin(x)(2x+2) + (x^2+2x)cos(x)} \neq \textcolor{red}{cos(x)( 2x + 2)}$.

This can be seen in the following graphs. $f'(x)$ represents the correct derivative of $f(x)$ because the critical points and positive and negative values match the original functions.

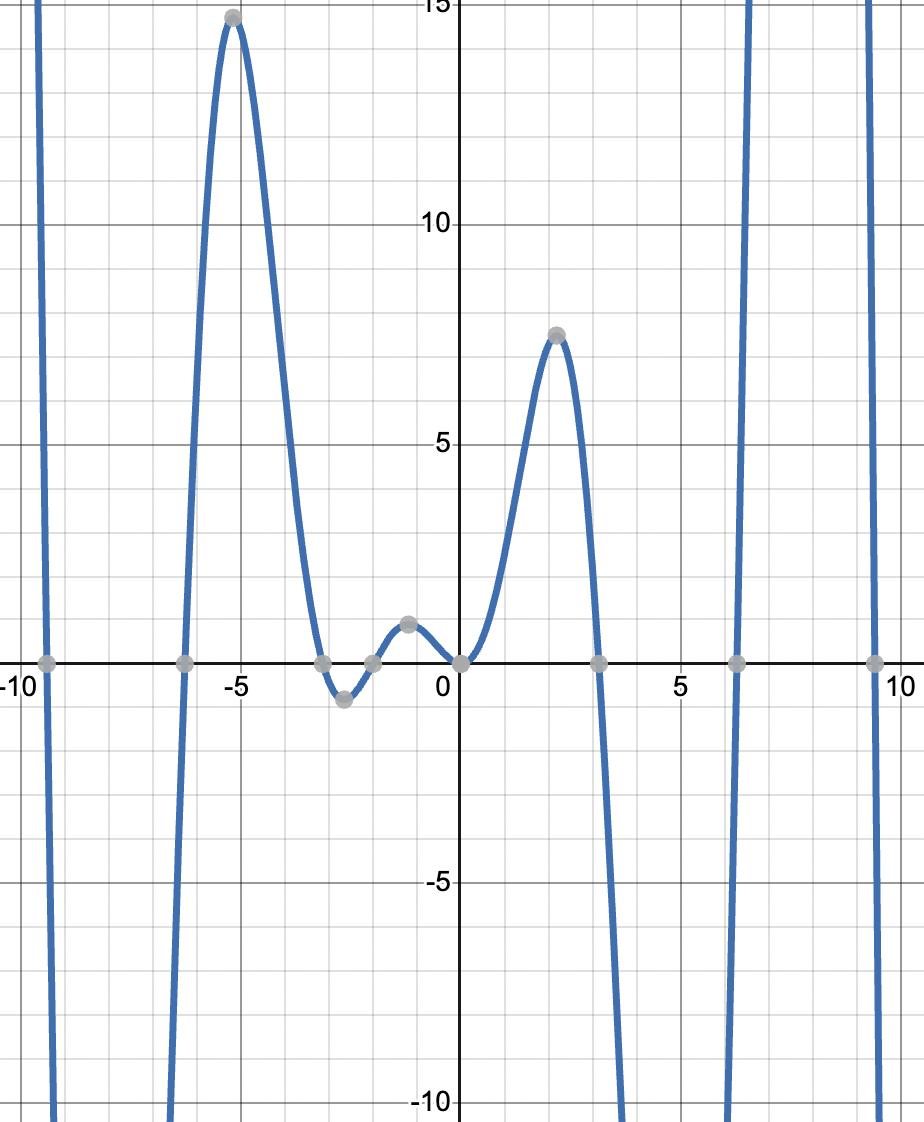
Graph of $f(x)$ created with Desmos

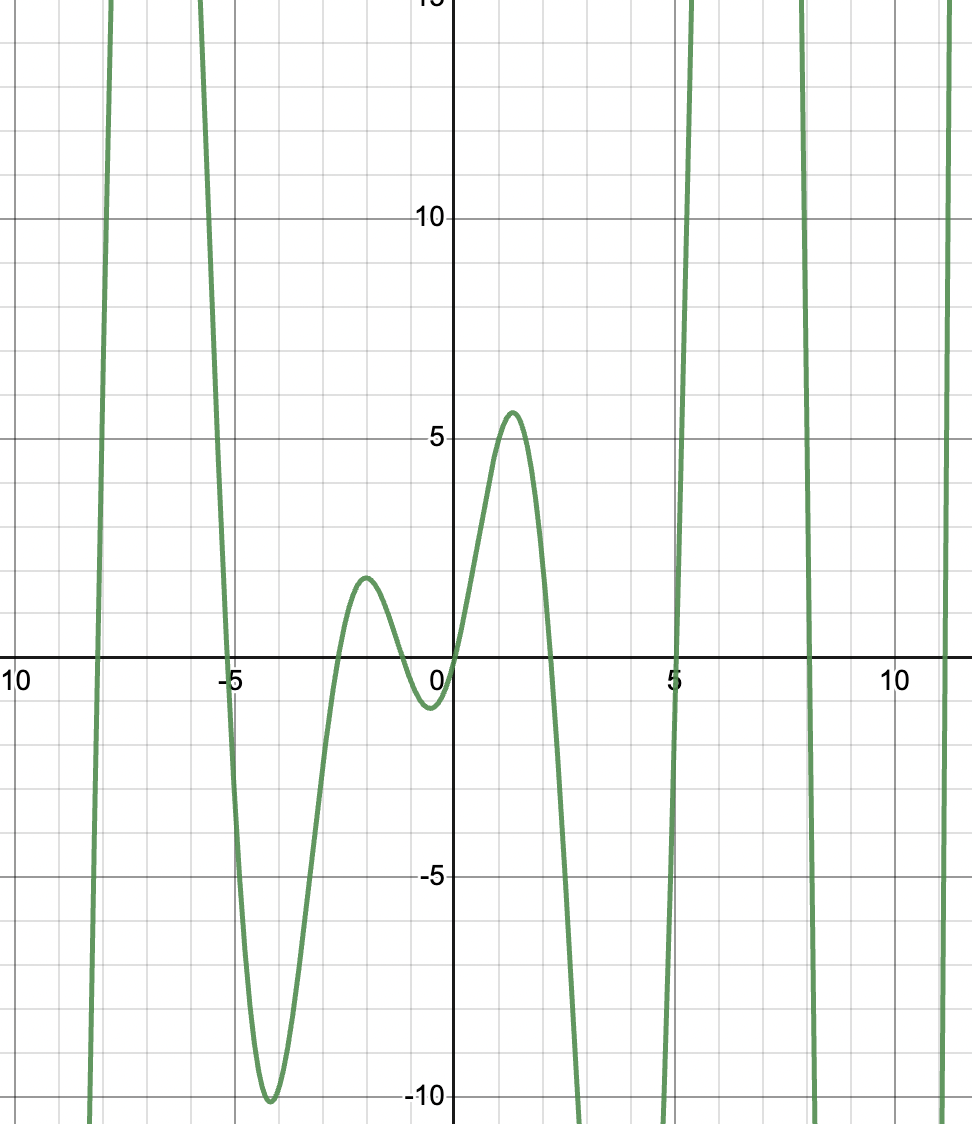
Graph of $f'(x)$ created with Desmos

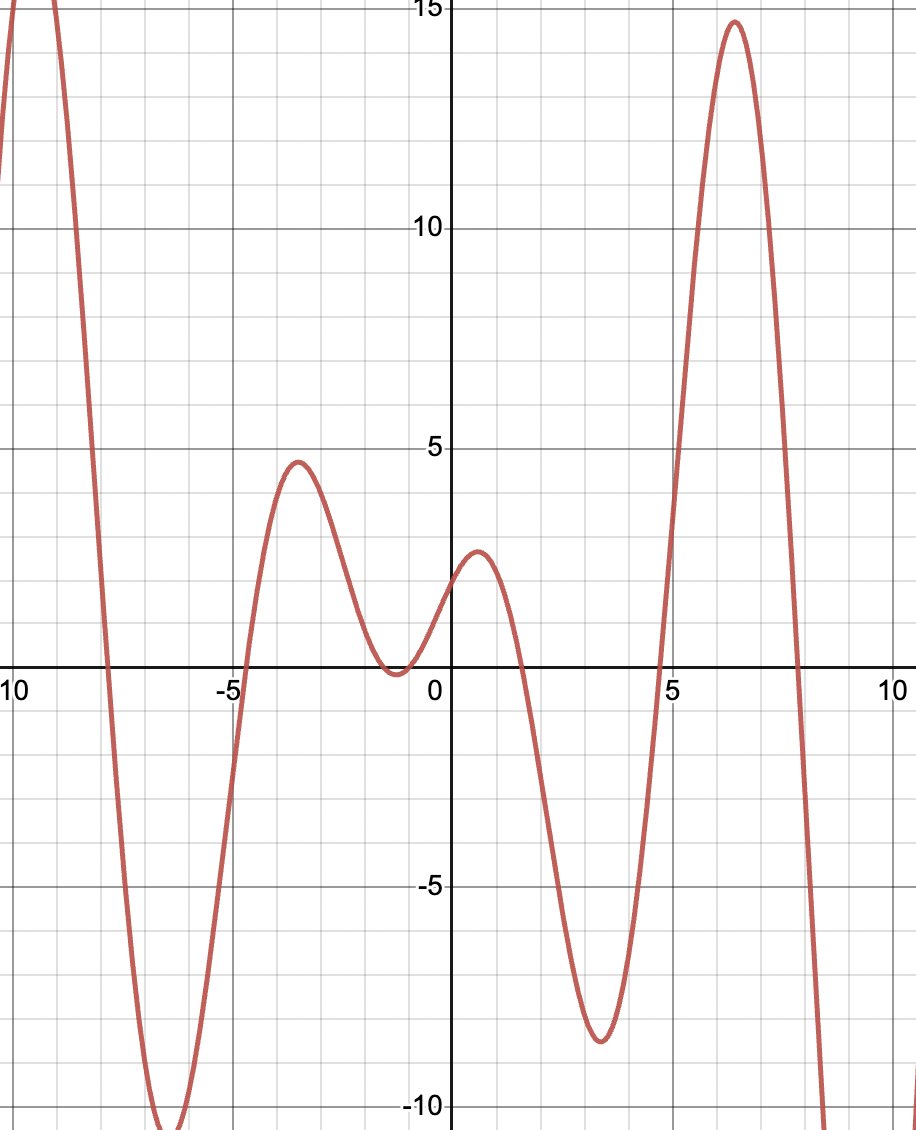
Incorrect Graph of $f'(x)$; Graph created with Desmos

---

🧮 Product Rule: Practice Problems

Let’s work on a few questions and make sure we have the concept down!

Product Rule: Example 1

Find $y'$ for $y = (3x^2-4x)(2x-1)$ with and without the Product Rule.

Solving Example 1 Without Product Rule

To find $y'$ without the product rule, we have to first expand the function.

Now we can take the derivative, using the derivative sum rule. Therefore,

Solving Example 1 With Product Rule

We can quickly use the product rule to solve for $y'$.

Therefore,

Unless specified, you do not have to simplify for the AP Calculus Exam, so this answer is perfectly acceptable! ✅

Product Rule: Example 2

Find $f'(x)$ if $f(x) = \sin(x)(3x^2 - 2x + 5)$.

Let's use the product rule to find the derivative of $f(x)$. Don’t forget, the derivative of $\sin(x)$ is $\cos(x)$! Brush up on your trig derivatives with this Fiveable guide: Derivatives of cos x, sinx, e^x, and ln x.

Therefore,

Product Rule: Example 3

Find $y'$ if $y = e^x\sin(x)$

Remember that the derivative of $e^x$ is still $e^x$! Now we can use the product rule.

Therefore,

---

🌟 Closing

Great work! 🙌 The product rule is a key foundational topic for AP Calculus. You can anticipate encountering questions involving the product rule on the exam, both in multiple-choice and as part of a free response.

Image Courtesy of Giphy