4.2 Straight-Line Motion: Connecting Position, Velocity, and Acceleration

4.2 Straight-Line Motion: Connecting Position, Velocity, and Acceleration

You might be wondering now that you are a master at calculating all kinds of derivatives under what scenarios you might need this knowledge. One of the many ways we can apply derivatives to real life is through solving rectilinear motion problems involving position, speed, velocity, and acceleration. 🚗

---

🌊 Derivatives and Motion

How is this possible? Well, remember from previous units that the derivative is used to determine the instantaneous rate of change or the rate of change of a function at a specific point. This means that…

🛥️Velocity and Speed

If we have a function that represents the position of an object as a function of time, $x(t)$, its derivative, $x'(t)$, would represent the velocity of the object at a specific point in time. You may also see $x'(t)$ written as $v(t)$ since the definition of velocity is the rate of change of position with respect to time. The instantaneous velocity is always signed.

When velocity is negative, the object is moving to the left: ➖ = ⬅️.

When velocity is positive, the object is moving to the right: ➕ = ➡️.

If we want just the speed, we simply take the magnitude (absolute value) of the velocity.

🚤Acceleration

Similarly, the derivative of a function that represents the velocity of an object describes the acceleration of the object at a specific point in time since acceleration is defined as the rate at which an object changes its velocity. Furthermore, since the first derivative of an object’s position is the object’s velocity and the first derivative of an object’s velocity is the object’s acceleration, we find that the second derivative of a function that represents the position of an object also describes the acceleration of the object at a specific point in time.

If the acceleration is positive that means that the velocity is increasing in the direction of the motion over time, and if the acceleration is negative that means that velocity is decreasing in the direction of the motion over time. And if the acceleration is zero that means that the object is moving at a constant rate.

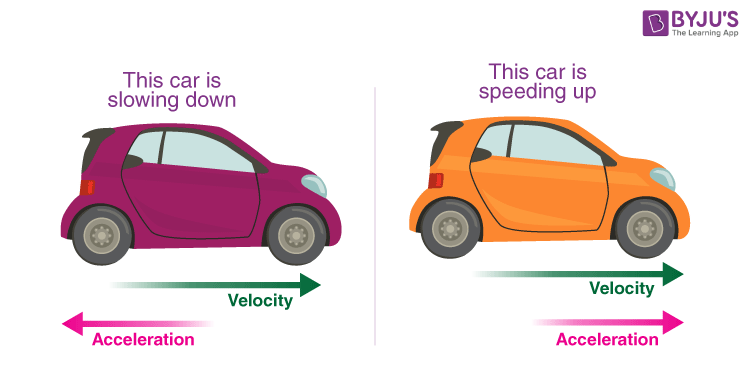
Image Courtesy of BYJU’S

You can also think of it like this:

When $v(t)$, $a(t)$ have the same sign, then the particle is speeding up! ➕➕ = ⬆️

When $v(t)$, $a(t)$ have different signs, then the particle is slowing down! ➕➖ = ⬇️

---

📝Rectilinear Motion: Practice

Let’s put this knowledge into practice!

❓Rectilinear Motion: Problems

Question 1:

A particle moves along the x-axis. The function $x(t)$ gives the particle’s position at any time $t >= 0$.

What is the particle’s acceleration $a(t)$ at $t=3?$

Question 2:

A particle moves along the x-axis. The function $x(t)$ gives the particle’s position at any time $t >= 0$.

What is the particle’s velocity $v(t)$ at $t=4?$

✅ Rectilinear Motion: Solutions

Question 1:

Acceleration is the rate of change of velocity, which is the rate of change of position. This means that we need to find the second derivative of the given position function $x(t) = 13t-9$ to find the acceleration of the particle at the given specific point in time:

$a(t) = x''(t) = \frac{d}{dt}[\frac{d}{dt}[13t-9]]=0$.

The particle's acceleration is constant at 0 for all $t >= 0$, so the particle’s acceleration at $t=3$ is 0.

Question 2:

Velocity is the rate of change of position, which means that we need to find the derivative of the given position function $x(t) = 4t^2-3t+16$ to find the velocity of the particle at the given specific point in time:

$v(t) = x'(t) = \frac{d}{dt}[4t^2-3t+16]=8t-3$.

The particle's velocity is $v(t)=8t-3$ for all $t >= 0$, so its velocity at $t=4$ is $29$.

Great work!