<< Hide Menu
5.6 Determining Concavity of Functions over Their Domains
At this point, you should know from the previous sections that the first derivative of a function can tell you a lot of information about the function, such as where it increases or decreases and where there is a minimum or maximum. Well, can the second derivative of a function tell us any information about the function? Yes, it can! Let’s learn about how we can determine the concavity of a function using its second derivative. ⬇️
🧗♀️ Determining Concavity
First off, what is concavity? In calculus, a function is said to be concave up if it faces upward and concave down if it faces downward. More technically speaking…
- If the slopes of the lines tangent to the function are increasing or the function’s derivative is increasing, then the function is concave up.
- If the slopes of the lines tangent to the function or the function’s derivative is decreasing, then the function is concave down.
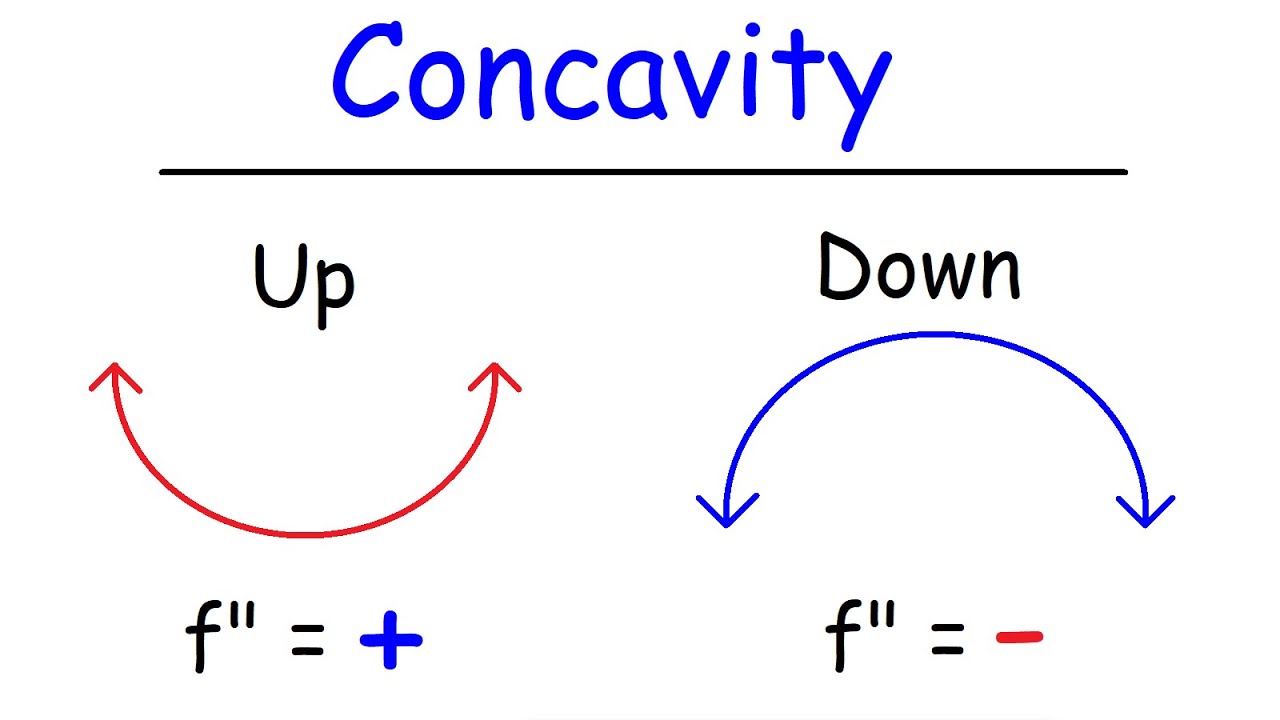
Image Courtesy of The Organic Chemistry Tutor
🥈 The Second Derivative
Based on this definition of concavity, we can start to see how concavity can be determined by analyzing the second derivative of a function. We can think of a function’s second derivative as the derivative of its first derivative. Remember higher-order derivatives?
So, since an increasing first derivative indicates concave up, a positive second derivative indicates concave up. Similarly, as a decreasing first derivative indicates concave down, a negative second derivative indicates concave down.
The point where the function switches concavity is called the inflection point. Because the function’s first derivative switches direction (goes from increasing to decreasing or vice versa) at this point, the function’s second derivative switches signs at this point. Thus, if the second derivative of a point is zero, then the point is a possible inflection point of the original function.
☀️ To sum these key points up…
- A graph is concave up if is increasing, and a graph is concave down if is decreasing.
- If is positive, then the function is concave up. If is negative, then the function is concave down.
- A point of inflection is a point where changes concavity and . If you only know , you have a possible point of inflection.
Now that you have all this information, let’s give a question a try!
✏️ Concavity Walkthrough
Consider the following function:
a) Determine the intervals where is concave up and concave down.
b) Find where has points of inflection.
Walkthrough of Part A
To determine whether is concave up or down, we need to find the intervals where is positive (concave up) or negative (concave down).
Let’s first find the first derivative and second derivative using the power rule.
We have the second derivative! To understand the behavior of over an interval, it is helpful to find a possible inflection point. Remember, a possible inflection point occurs where .
Great! There is a possible point of inflection at . This point divides the function into two intervals, and . Remember when we evaluated the sign of the function in the last key topic? We essentially want to do the same here to determine concavity.
Let’s test …
Since , the interval to the left of is concave down.
Now let’s test …
Since , the interval to the right of is concave up.
✏️ Therefore, our answer to part a is the following: “ is concave down on the interval and concave up on the interval .”
Walkthrough of Part B
For part b, all we have to do is see if our possible point of inflection at is an actual point of inflection. In order for this to be true, has to change concavity at .
We found out that it does in part a! Therefore, has a point of inflection at because changes concavity and at this point.
📝 Concavity Practice Problems
Give these two questions a try!
❓ Concavity Practice Problems
Question 1: Let . What is the concavity of at ?
Question 2: Let . What is the concavity of at ?
✅ Concavity Answers and Solutions
Question 1:
To evaluate the concavity of a function at a point, we need to determine the second derivative of the function at the point.
is equal to at .
Since is positive, is concave up at .
Question 2:
To evaluate the concavity of a function at a point, we need to determine the second derivative of the function at the point.
is equal to at .
Since , might be a point of inflection. To check whether it truly is a point of inflection, we can evaluate the second derivative of the function on both sides of the point to see if it changes sign or not. If the sign switches, then it is a point of inflection.
| Concavity | ||
| Concave up | ||
| Concave down |
Since the second derivative’s sign switches, meaning the function’s concavity changes, is a point of inflection.
⭐ Closing
Great work! Understanding concavity is an important aspect of analyzing and understanding the behavior of a function and can be used to make predictions and draw conclusions about the function's behavior.
Happy calculus studying! 🤓

© 2024 Fiveable Inc. All rights reserved.