<< Hide Menu
5.3 Determining Intervals on Which a Function is Increasing or Decreasing
4 min read•june 18, 2024
5.3 Determining Intervals on Which a Function is Increasing or Decreasing
What can the derivative of a function show us about the function itself? Can it tell us when the function increases or decreases? Yes, it can! In this lesson, we’ll delve into how we can use derivatives to determine when a function increases or decreases. 📈
🕑 When Does a Function Increase or Decrease?
In order to determine the intervals on which a function is increasing or decreasing, we first need to understand the concept of the derivative. The derivative of a function is the rate of change of the function at a given point.
Thus, we know the following:
- ➕=📈 If the derivative is positive at a certain point (which means the rate of change is positive at that point), the function is increasing at that point.
- ➖=📉 If the derivative is negative at a certain point, the function is decreasing at that point.
Take a look at this graph to see these trends in action. The gray line represents the function, , and the black line represents its derivative, .
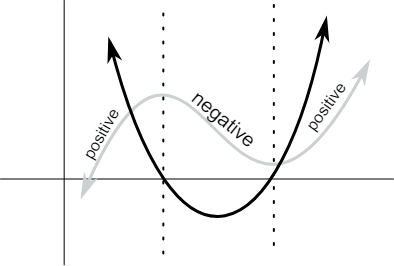
Image Courtesy of Informal Calculus
Now, you may be thinking that finding the interval where a function is increasing or decreasing is as simple as finding the interval where the function’s derivative is positive or negative, respectively. Well, it is! 🪄
Where can a function change from increasing to decreasing and vice versa? It can only change its direction from increasing to decreasing and vice versa at its critical points, points where the function’s derivative equals or is undefined, and the points where the function itself is undefined.
So, for each of the intervals defined by the points where the function can change behavior, we can determine whether the function is increasing or decreasing on the interval by just plugging a point on that interval into the function’s derivative and seeing if the result is positive or negative. If it’s positive, then the function is increasing on that interval; if it’s negative, then the function is decreasing on that interval. Let’s give it a try!
✏️ Function Behavior: Walkthrough
➡️ Let be a function defined for all real numbers except Also let be defined as . On which intervals is increasing?
From what we learned above, we can analyze the intervals where is increasing by looking for the intervals where its derivative is positive.
A function can only change its direction from increasing to decreasing and vice versa at its critical points and the points where the function itself is undefined. Based on the problem statement, we determine that in this case, the only points where can change direction are and . We determine this by doing the following and solving:
at so it is a critical point and is undefined at as stated in the problem.
These two points divide the number line into three intervals:
Let’s evaluate at each interval to see if it’s positive or negative on that interval and therefore see if is increasing or decreasing on the interval. To evaluate on an interval, we can choose any -value within the interval to substitute with and calculate.
In the table below, you’ll notice that we chose for the first interval, for the second interval, and for the third! Plug in, solve, and determine the behavior of the function.
| Interval | Verdict | ||
| is decreasing | |||
| is increasing | |||
| is increasing |
In conclusion, is increasing on the intervals and .
🪜 Steps to Determining Function Behavior
Here are the steps we used if you prefer seeing them in list form:
- 🎯 Determine the critical points of the function, where equals zero or is undefined.
- 🔢 Divide the function's domain into intervals based on the critical points determined. This is where you break the number line into pieces to see its behavior!
- 🔨 For each interval, choose a test point within that interval.
- ✏️ Evaluate the function's derivative at the chosen test point.
- 🏁 Interpret the result.
- If the result is positive, the function is increasing on that interval.
- If the result is negative, the function is decreasing on that interval.
Now you can put these steps into practice!
📝 Function Behavior: Practice Problems
Time to solve some problems! 🔍
❓ Function Behavior: Problems
Function Behavior: Question 1
Let .
On which interval(s) is decreasing?
Function Behavior: Question 2
Let .
On which interval(s) is increasing?
✅ Function Behavior: Answers and Solutions
Function Behavior: Question 1
The answer to this problem is . Let’s get into why. ⬇️
We can analyze the intervals where is decreasing by looking for the intervals where its derivative is negative.
A function can only change its direction from increasing to decreasing and vice versa at its critical points and the points where the function itself is undefined. So first, take the derivative and find the critical points.
Since the derivative of is , the only points where can change direction are and as at only these points.
These two points divide the number line into three intervals: .
Let’s evaluate at each interval to see if it’s positive or negative on that interval and therefore if is increasing or decreasing on the interval.
| Interval | Verdict | ||
| is increasing | |||
| is decreasing | |||
| is increasing |
In conclusion, is decreasing on the interval .
Function Behavior: Question 2
The answer to this problem is and . Here’s why:
We can analyze the intervals where is increasing by looking for the intervals where its derivative is positive.
A function can only change its direction from increasing to decreasing and vice versa at its critical points and the points where the function itself is undefined.
Since the derivative of is , which we can rewrite as , the only points where can change direction are , , and as at only these points.
These three points divide the number line into four intervals: .
Let’s evaluate at each interval to see if it’s positive or negative on that interval and therefore if is increasing or decreasing on the interval.
| Interval | Verdict | ||
| is decreasing | |||
| is increasing | |||
| is decreasing | |||
| is increasing |
In conclusion, is decreasing on the intervals and .
⭐ Closing
Great work! You now have the steps and practice to determine where a function changes from increasing to decreasing.

© 2024 Fiveable Inc. All rights reserved.