5.1 Using the Mean Value Theorem

5.1 Using the Mean Value Theorem

In the previous unit, we learned all about applying derivatives to different real-world contexts. What else are derivatives useful for? Turns out, we can also use derivatives to determine and analyze the behaviors of functions! 👀

📈  Mean Value Theorem

The Mean Value Theorem states that if a function f is continuous over the interval $[a, b]$ and differentiable over the interval $(a, b)$, then there exists a point $c$ within that open interval $(a,b)$ where the instantaneous rate of change of the function at $c$ equals the average rate of change of the function over the interval $(a, b)$.

In other words, if a function f is continuous over the interval $[a, b]$ and differentiable over the interval $(a, b)$, there exists some $c$ on $(a,b)$ such that $f'(c)=\frac{f(b)-f(a)}{b-a}$.

Image Courtesy of Sumi Vora and Ethan Bilderbeek

Yet another way to phrase this theorem is that if the stated conditions of continuity and differentiability are satisfied, there is a point where the slope of the tangent line is equivalent to the slope of the secant line between $a$ and $b$.

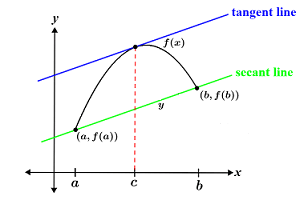
Image Courtesy of Math.net

Remember from Unit 1, to be continuous over $[a, b]$ means that there are no holes, asymptotes, or jump discontinuities between points a and b. Because the interval contains closed brackets, the graph must also be continuous at points $a$ and $b$.

Additionally, if we recall from previous guides, to be differentiable over $(a, b)$ means that the function is continuous over the interval and that for any point $c$ over the interval, $\lim_{x\to c} \frac{f(x) - f(c)}{x - c}$ exists.

✏️ Mean Value Theorem: Walkthrough

We can use the Mean Value Theorem to justify conclusions about functions by applying it over an interval. For example:

Let $f$ be a differentiable function. The table gives its selected values:

Can we use the Mean Value Theorem to say the equation $f'(x)=5$ has a solution where $3< x<9$?

Since it is given that $f$ is differentiable, we can apply the Mean Value Theorem (MVT) on the interval $(3,9)$. This is what we should write out!

Since $f$ is continuous and differentiable on $(3,9)$, MVT can be applied. The MVT states that there exists a $c$ on $(3,9)$ such that $f'(c)=\frac{f(9)-f(3)}{9-3}=\frac{44-20}{9-3}=\frac{24}{6}=4.$

$4 \neq 5$ so MVT cannot be used to say that $f'(x)=5$ has a solution.

---

📝 Mean Value Theorem: Practice Problems

Now, it’s time for you to do some practice on your own! 🍀

❓ Mean Value Theorem: Practice

Question 1: Mean Value Theorem

Let $h(x)=x^3+3x^2$ and let $c$ be the number that satisfies the Mean Value Theorem for $h$ on the interval $[-3,0]$.

What is $c?$

Question 2: Mean Value Theorem

Let $f$ be a differentiable function. The table gives its selected values:

Can we use the Mean Value Theorem to say the equation $f'(x)=2$ has a solution where $2<x<9$?

✅ Mean Value Theorem: Answers and Solutions

Question 1: Mean Value Theorem

Since $h$ is a polynomial, $h$ is continuous on $[-3,0]$ and differentiable on $(-3,0)$. Therefore, the Mean Value Theorem can be applied. By the Mean Value Theorem, there exists a $c$ on $(-3,0)$ such that…

To find $c$, we need to differentiate $f(x)$ and find $c$ such that $f'(c)=0.$

By the quadratic formula, we have $x=-2,0$.

Since only $x=-2$ is in the interval $(-3,0)$, $c=-2.$ Great work! Make sure you remember to check if the value(s) you get are in the given interval.

Question 2: Mean Value Theorem

Since it is given that $f$ is differentiable, we can apply the Mean Value Theorem (MVT) on the interval $(2,9)$.

The MVT states that there exists a $c$ on $(2,9)$ such that $f'(c)=\frac{f(9)-f(2)}{9-2}=\frac{35-14}{9-2}=\frac{21}{7}=3.$ $3 \neq 2$ so MVT cannot be used to say that $f'(x)=2$ has a solution.

---

💫 Closing

The Mean Value Theorem states that for any continuous function on a closed interval, there exists a value c in the interval such that the value of the derivative of the function at c is equal to the average rate of change of the function over the interval. By using this theorem, we can find the mean value of a function on a given interval, which can provide useful information about the behavior of the function. 🧐