8.6 Finding the Area Between Curves That Intersect at More Than Two Points

8.6 Finding the Area Between Curves That Intersect at More Than Two Points

Welcome back to AP Calculus with Fiveable! In the last two study guides, we discussed how to find the area between curves expressed as functions of $x$ and as functions of $y$. Today, we’re going to apply what we know from those key topics to curves that intersect at more than two points! 🧠

📏 Understanding Finding Area Between Curves

In calculus, finding the area between curves intersecting at more than two points is crucial. This technique involves calculating the definite integral of the absolute value of the difference between the two curves over a given interval. The formula for the area between two curves $y=f(x)$ and $y=g(x)$ from $x=a$ to $x=b$ is given by:

Any negative regions are guaranteed to be considered by the absolute value. We can calculate the area between the curves inside the given interval using this approach.

🪜 Finding Area Between Intersecting Curves Steps

Here are some steps you can take when approaching questions asking you to solve for the area between two curves that intersect at more than two points:

1. 👀 Identify the points of intersection by setting the two equations equal to each other.
2. 📈 Optional, but highly recommend: graph the functions.
3. 🤔 Identify what approach to take (top-bottom with vertical slices, or right-left with horizontal slices).
4. 🔢 Set up the integral with different intervals based on intersection points.
5. 💯 Evaluate the integrals to find the area.

Let’s go step by step and walk through an example!

🤓 Area Between Curves Walkthrough

Find the area between the curves $y = x^3-2x^2$ and $y=x^2-2x$ between the interval $0\le x \le 2$.

👀 Step 1) Identify the points of intersection.

To find the points of intersection, we set our two equations equal to each other, like so:

Now simplify to find the points! 🕵️

We now know that these two functions intersect at $x=0, 1, 2$.

📈 Step 2) Graph the functions.

This helps you visualize what is going on and identify which approach to take in the next step.

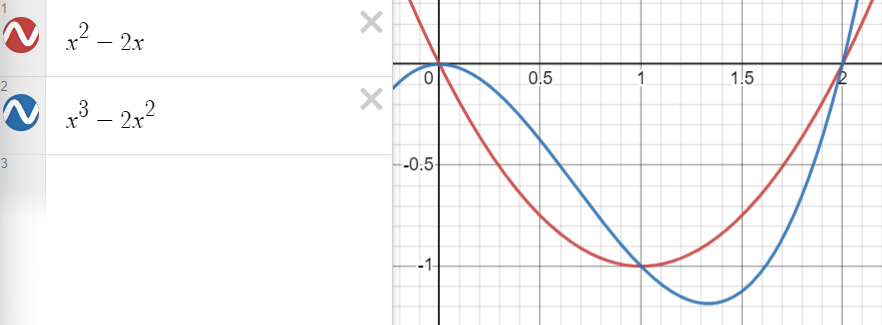
Image Created with Desmos

🤔 Step 3) Identify what approach to take

Taking a look at the graph, the curves are on top of one another. Therefore, we can use vertical slices and subtract the bottom function from the top function.

In the interval $0 \le x \le1$, we have $x^3−2x^2$ as our $f(x)$ in the blue and $x^2−2x$ as our $g(x)$ in the red.

Vice versa is true in the interval $1\le x \le2$, since the red curve in the graph above is on top of the blue curve.

🔢 Step 4) Set up the integral with different intervals

So we set up our integral accordingly!

💯 Step 5) Evaluate the integrals to find the area.

Great work! 🙏

---

👩‍🏫 Area Between Curves Practice

Your turn to try a question!

Find the area between $3x^2-x^2-10x$ and $-x^2+2x$ between the interval $-2 \le x \le 2$.

✏️ Solution to Practice Problem

First, set the two equations equal to find the points of intersection. ⬇️

$\therefore$ our points of intersection are -2, 0, and 2.

Anddd…here’s the graph of these two functions, so you can determine which approach to take.

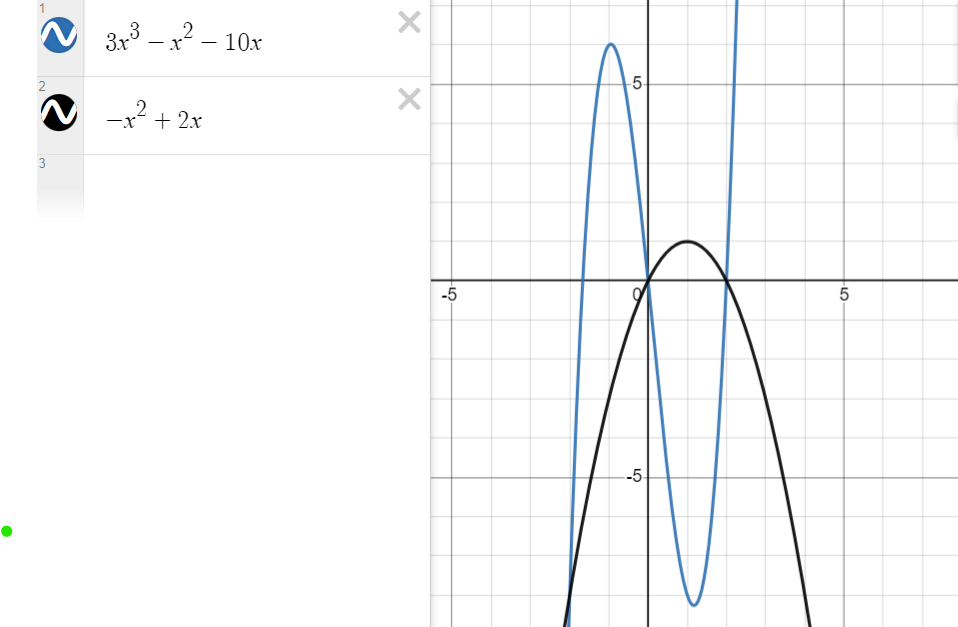
Image Created with Desmos

Since the functions are on top of each other, we can set up the integrals with vertical slices in mind.

Great work!

---

🕺Closing

This walkthrough and practice problems aimed to demystify the process, providing step-by-step guidance on how to approach such problems! We hope you feel more comfortable with the process. 😊

Remember to carefully consider the intervals and points of intersection to calculate the area enclosed by the curves accurately. Happy learning!