<< Hide Menu
8.8 Volumes with Cross Sections: Triangles and Semicircles
5 min read•june 18, 2024
8.8 Volumes with Cross Sections: Triangles and Semicircles
Recall from the last guide that we can instead break up 3D objects bound by curves into infinitely thin slices that are easier to work with. In this guide, we’ll apply this concept to triangles and semicircles!
🪩 Solids with Cross Sections: Review
To find the volume of a solid with known cross-sections we can use the formula
where is a function for the area of a cross-section (some two-dimensional shape) perpendicular to the x-axis on the closed interval and represents its thickness. In this guide, we’ll explore this same concept using different shapes.
🔺Triangular Cross Sections
The formula for the area of a triangle depends on what kind of triangle it is. This means that the function for a solid with triangular cross sections will be different depending on the kind of triangle that makes up the cross sections of the solid. We will develop volume formulas for solids with equilateral and right-angled isosceles triangle cross sections.
🔻 Equilateral Triangles
The formula for the area of an equilateral triangle is given by the equation where is the length of one of the sides of the triangle. This means that the formula for the volume of a solid with equilateral triangle cross sections is given by .
📐 Right Isosceles Triangles
The formula for the area of a right-angled isosceles triangle is were is the length of the two matching sides of the triangle. So for a solid with right isosceles triangle cross sections, its volume will be given by formula .
🚫 Semicircular Cross Sections
To find the area of a circle, we can use the familiar formula , where is the radius of the circle. A semicircle only has half the area of a circle though, so we’ll use the equation for A(x) in our volume formula. That means that for a solid with semicircular cross sections, its volume will be found using the equation .
🧠 Solving Cross-Section Problems
Now that we have our area functions we need to find or in order to use them! Let’s work though an example.
Suppose a region bounded by and forms the base of a solid with cross sections taken perpendicular to the x-axis. What integral will give the volume of the solid if the cross sections are equilateral triangles? What about semicircles?
Question courtesy of Flipped Math
🧐We’ll begin by drawing a picture of out graphs so we can visualize the problem and identify the bounds we’ll use when evaluating our integral.

Image courtesy of Flipped Math
In this image, forms the upper curve, and is the bottom curve. Let’s let function and . The area in grey is the base of our solid. The purple line represents a singular cross section of this solid. You can imagine that the cross section is coming towards you along a z-axis not shown in this drawing. If we rotated our graph and included the z-axis, our graph would look like the one on the top for equilateral triangle cross sections and the one on the bottom for semicircular cross sections.
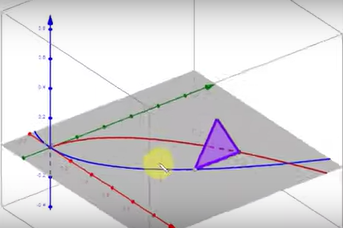
Image courtesy of Flipped Math
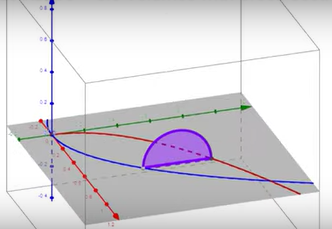
Image courtesy of Flipped Math
Identifying bounds
👀Graphically, we can see that the two functions intersect for and . This means that our bounds are given by the closed interval [0, 1]. We could also find the bounds algebraically by setting the two functions equal and solving for x as shown below.
🔺 Equilateral Triangle
Finding the Side Length
You’ll notice that one side of the equilateral triangle at a point is given by . So, the side length of the equilateral triangle cross section is given by .
Setting up Cross Section Area Functions
Now that we have a value for , we can identify our functions for this solid. For the equilateral triangle, this will be given by .
Building the Volume Integral
🪢 Let’s tie it all together now and find our volume integrals. Plugging in our bounds and functions into the formula , we find that the volume of the solid with equilateral triangle cross sections is .
Solving
🚫 Semicircle
Finding the Radius
The diameter of the semicircle at a point is defined by . Recall that the radius of a circle is one half its diameter. Therefore, the radius of the semicircle for some is .
Setting up Cross Section Area Functions
Now that we have a value for , we can identify our functions for this solid. For the semicircle, this will be given by .
Building the Volume Integral
🪢 Let’s tie it all together now and find our volume integrals. Plugging in our bounds and functions into the formula , we find that the volume of the solid with semicircular cross sections is given by .
Solving
📝Summary
When finding the volume of a solid with a known cross section, we can use the equation
is a function for the area of a cross section perpendicular to the x-axis on the interval [a, b].
For equilateral triangle cross sections where is the length of one of the sides of the triangle.
For right isosceles triangle cross sections were is the length of the two matching sides of the triangle.
For semicircular cross sections where is the radius of the semicircle at .
Using methods for finding the areas between curves we can determine equations to describe or and find bounds for our integral.
Plugging in our bounds and the function results in the volume integral for the solid. Evaluating this definite integral will give a value for the volume of the solid.

© 2024 Fiveable Inc. All rights reserved.