7.6 Sorting

The other major application of ArrayLists is sorting, which is placing elements in an ascending or descending order, but it is mainly used for ascending order. There are many sorting algorithms, but we'll only learn selection sort and insertion sort in this unit and merge sort in Unit 10. There are many others that you can view in this video:

🎥 Video on 50+ Sorts, Visualized - Bar Graph *Seize Warning*

Courtesy of Musicombo.

Determining Whether An ArrayList is Sorted

To determine whether an ArrayList is sorted, there is a quick algorithm that sees if the elements are always increasing. Here is its implementation:

/** Returns if the ArrayList is sorted in ascending order */ public static boolean isSorted(ArrayList<Integer> array) { for (int i = 0; i < array.size() - 1) { if (array.get(i + 1) < array.get(i)) { //checks if two array elements are in the return false; // wrong order } } return true; }

Selection Sort

Selection sort is the simpler of the two sorting algorithms. The selection sort divides the ArrayList into two "subarrays:" the first being a sorted subarray and the second being the unsorted subarray.

Here is the implementation preceded by pseudocode which explains why it's called the selection sort:

/** Uses selection sort on an ArrayList * 1. Originally the ArrayList is unsorted * 2. We select the smallest number and swap it with the first element * 3. Now the sorted subarray is the first item and the rest of the array is unsorted * 4. Select the smallest of the unsorted numbers (the second smallest overall) and * swap it with the second element * 5. Now the first two elements are sorted and the rest are unsorted * 6. Repeat until the rest of the elements are sorted */ public static ArrayList<Integer> selectionSort(ArrayList<Integer> array) { for (int i = 0; i < array.size() - 1; i++) { // traverse to the second to last item, the last item is automatically the largest int smallestIndex = i; int smallestElement = array.get(i); for (int j = i + 1; j < array.size(); j++) {

//traverse through the rest of the array, looking for the smallest remaining item (less than smallestElement) if (array.get(j) < smallestElement) { smallestIndex = j; smallestElement = array.get(j); } } if (smallestIndex > i) { // swap the elements of i and j if the element of i isn't already the smallest int originalItem = array.get(i); array.set(i, smallestElement); array.set(smallestIndex, originalItem); } } return array; }

Here is a visual graphic showing selection sort:

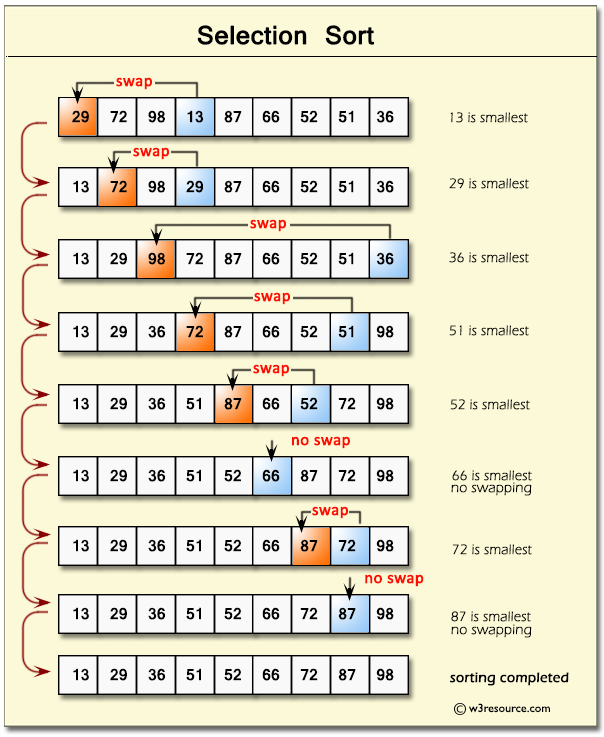
Courtesy of w3resource.

Insertion Sort

The other sorting algorithm is the insertion sort. Like selection sort, there are sorted and unsorted subarrays.

Here is the implementation and pseudocode explaining why it is called insertion sort:

/** Uses insertion sort on an ArrayList * 1. Assume the first element is already sorted * 2. Select the second element * 3. Insert it before the first element or keep it in place to make the first 2 elements sorted * 4. Select the third element and insert it so that the first 3 elements are sorted * 5. Repeat until all elements are sorted. */ public static ArrayList<Integer> insertionSort(ArrayList<Integer> array) { for (int i = 1; i < array.size(); i++) { int currentElement = array.get(i); int currentIndex = i; for (int j = i; j > 0; j--) { if (currentElement < array.get(j - 1)) { // shifting the item left until properly placed by swapping consecutive items int itemToRight = array.get(j - 1); array.set(j - 1, currentElement); array.set(j, itemToRight); } } } return array; }

Here is a visual version of insertion sort:

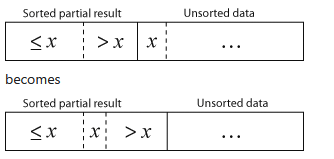
Courtesy of Wikipedia.

Informal Run-Time Comparisons

To compare the performance of these sorting algorithms, you can count the number of statements they execute during execution. For example, you might count the number of times the loop variables are updated or the number of times elements are compared or swapped. This will give you an idea of how many statements each algorithm executes to complete the sorting process.

Informal run-time comparisons of program code segments can be made using statement execution counts. By comparing the number of statements executed by different sorting algorithms, you can get a sense of their relative efficiency and make informed decisions about which algorithm to use in a given situation.

Selection sort requires more data accesses and modifications than insertion sort because it needs to search the entire array to find the minimum element on each iteration. Insertion sort, on the other hand, only needs to access and modify the data in the sorted portion of the array.

As a result, insertion sort may be faster for small data sets or when the data is partially sorted.