<< Hide Menu
Unit 6 FRQ (Simple Harmonic Motion) Answers
3 min read•june 18, 2024
AP Physics 1 Free Response Question Answers for Simple Harmonic Motion
👋 Welcome to the AP Physics Unit 6 FRQ (Simple Harmonic Motion) Answers. Have your responses handy as you go through the rubrics to see how you did!
⏱ Remember, the AP Physics 1 exam has 5 free-response questions, and you will be given 90 minutes to complete the FRQ section. (This means you should give yourself ~18 minutes to go through each practice FRQ.)
Setup
A group of students must determine the spring constant k of a spring that hangs vertically from a ring stand. The students attach a block to the bottom of the vertical spring, as shown in Figure 1. The students then pull the block-spring system 0.5 m below the system’s equilibrium position and release the system so that it oscillates. The students record the mass M of the block and the period of oscillation T for several trials, as shown in Table 1.
Figure 1
Table 1
| M (kg) | T (s) |
| 0.3 | 0.77 |
| 0.6 | 1.07 |
| 0.9 | 1.29 |
| 1.2 | 1.50 |
Questions with Answers & Rubric
Part A
The students want to determine the spring constant of the spring.
(i) Indicate below which quantities could be graphed to determine the spring constant of the spring by using a best-fit line. You may use the remaining columns in the table above, as needed, to record any quantities (including units) that are not already in the table. (1pt)
- 1pt: Vertical Axis: 4 * π^2 * m, Horizontal Axis: T^2
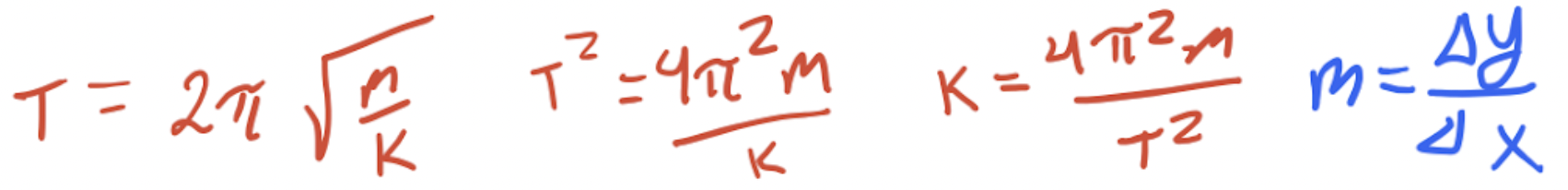
| M (kg) | T (s) | y = 4 * π^2 * m | x = T^2 |
| 0.3 | 0.77 | 11.8 | 0.5 |
| 0.6 | 1.07 | 23.7 | 1.14 |
| 0.9 | 1.29 | 35.5 | 1.66 |
| 1.2 | 1.50 | 47.3 | 2.25 |
📄 Additional Resources
- Study Guide: Period of Simple Harmonic Oscillators
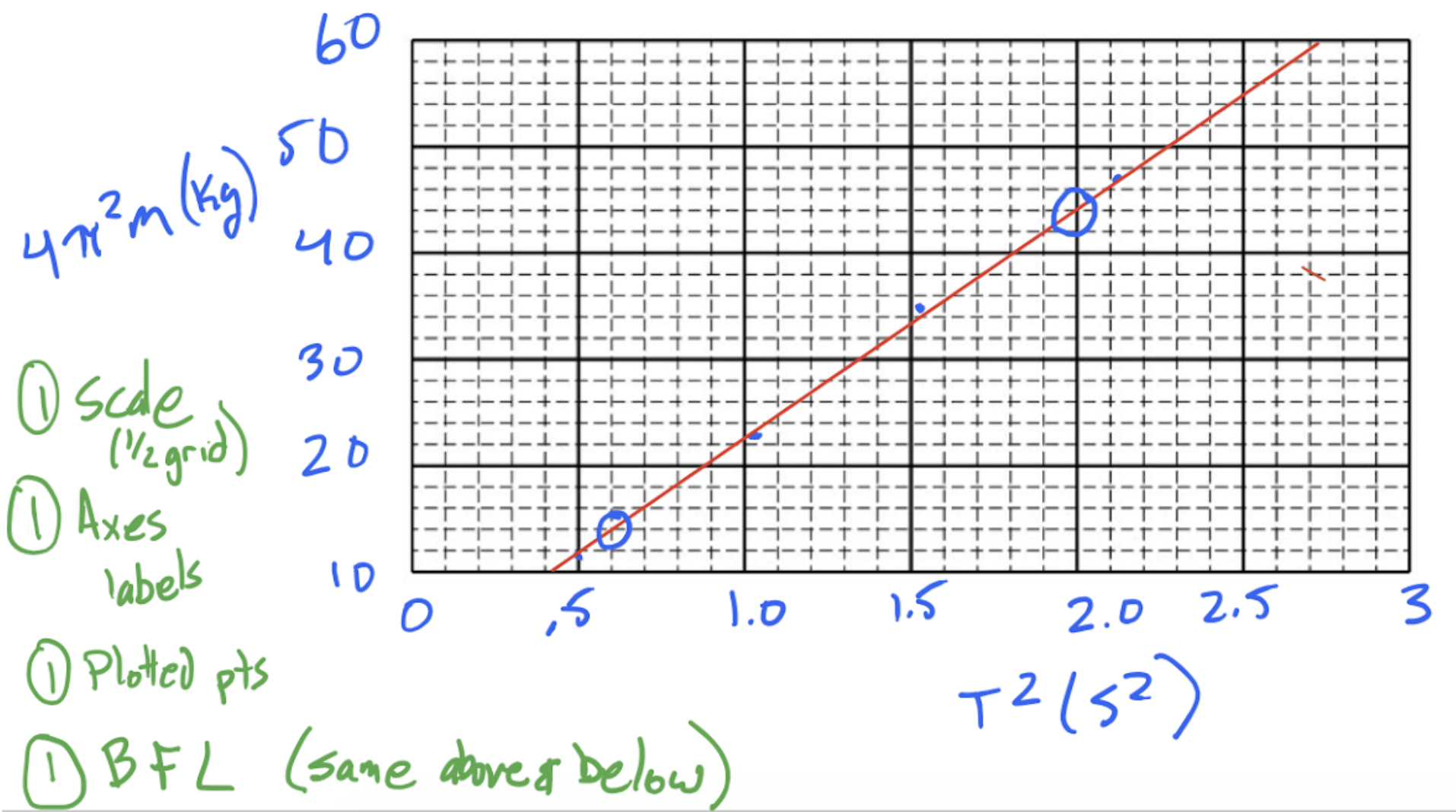
(ii) On the grid below, plot the appropriate quantities to determine the spring constant of the spring by using a best-fit line. Clearly scale and label all axes, including units as appropriate. (4pts)
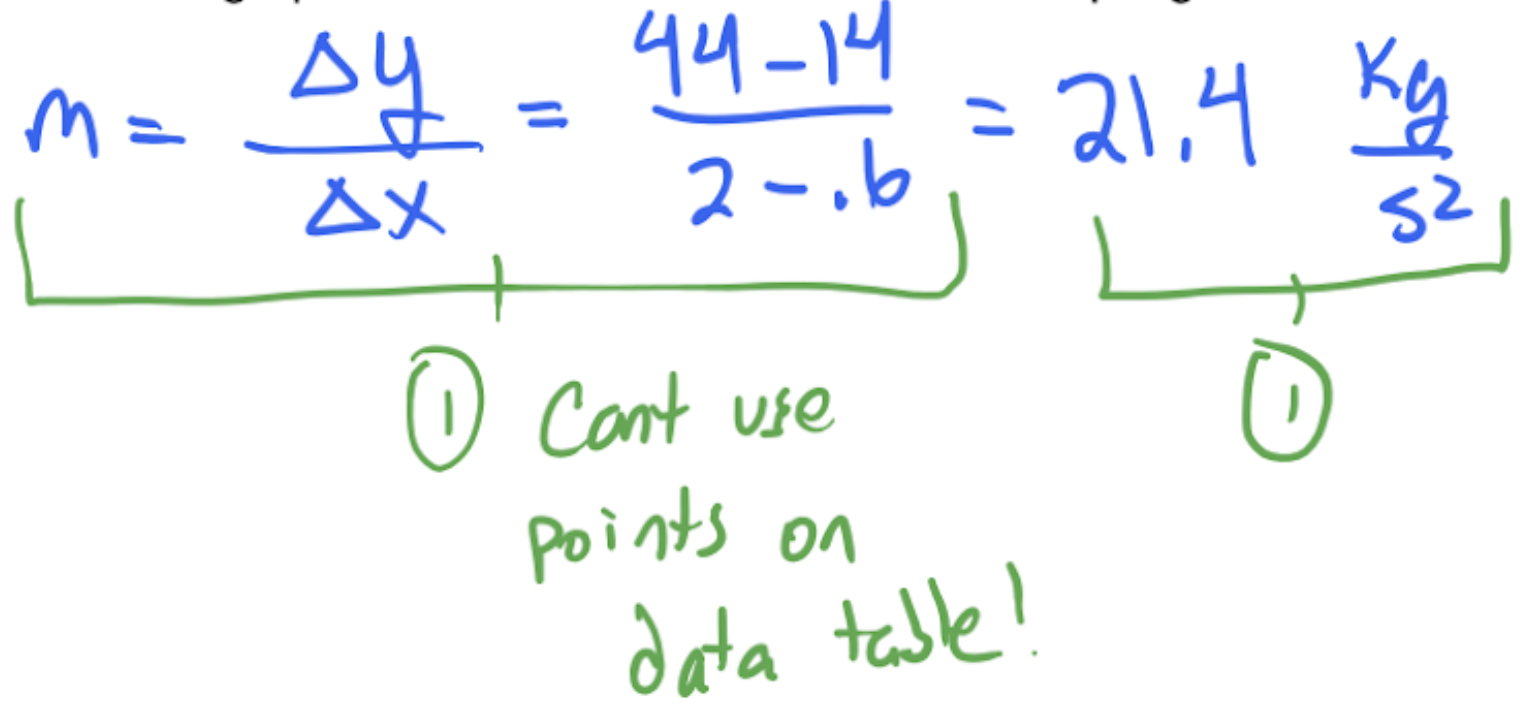
(iii) Use the graph above to estimate a value for the spring constant of the spring. (2pts)
Part B
Another group of students performs a similar experiment in which the same block-spring system from trial 1 oscillates, but in the horizontal direction, as shown in Figure 2. Frictional forces between the block and the surface are considered to be negligible. Furthermore, the students pull the block-spring system 0.8 m from the system’s equilibrium before they release the system so that it oscillates.
(i) Will this change in the experiment affect the value of the period of oscillation T for the block-spring system compared to the situation from part (a)? Briefly state your reasoning. (4pts)
- 1pt: No
- 1pt: T = 2π * sqrt(m/K)
- 1pt: The block is now horizontal, but the mass and spring constant are still the same.
- 1pt: From the equation, since gravity and amplitude don't matter, and since the mass and spring constant are the same, the period will not change.
Part C
(i) Describe an experimental procedure to determine whether or not the period of oscillation T for the block-spring system is different compared to the situation from part (a). Include any steps necessary to reduce experimental uncertainty. Give enough detail so that another student could replicate the experiment. As needed, include a diagram of the experimental setup. Assume equipment usually found in a school physics laboratory is available. (5pts)

- 1pt: Diagram above
- 1pt: Pull back the block so the stretch is 0.8m (measured by a meterstick).
- 1pt: Let go and time 10 oscillations (with a stopwatch).
- 1pt: Compare this period to the period found in (a)
- 1pt: Complete the results and average the resulting periods.
No graphs needed!
Next Steps
- 🧠 Want to continue reinforcing your knowledge of Unit 6? Check out Unit 6 Trivia, either as a document or as a game.
-
- 📚 Want to review multiple units? Check out all of the AP Physics 1 FRQs.

© 2024 Fiveable Inc. All rights reserved.