<< Hide Menu
Peter Apps
Peter Apps
As of 2021, College Board only tests Units 1-7 on the AP Physics 1 exam. This page's content will not be tested on the exam, but we kept it online for you all as a resource.
Enduring Understanding 1.B ⚡
Electric charge is a property of an object or a system that affects its interactions with other objects or systems containing the charge.
Essential Knowledge 1.B.1
The electric charge is conserved. The net charge of a system is equal to the sum of the charges of all the objects in the system.
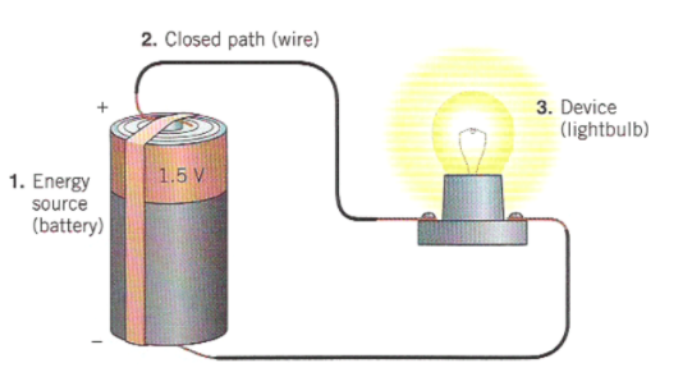
What is a Circuit?
A circuit is a closed loop of electrical current. If the loop is open or doesn’t allow the current to return to its starting position, electricity will not flow through the circuit and any devices on that partial loop will not work. Common ways of breaking a circuit include switches or blow / removed light bulbs.
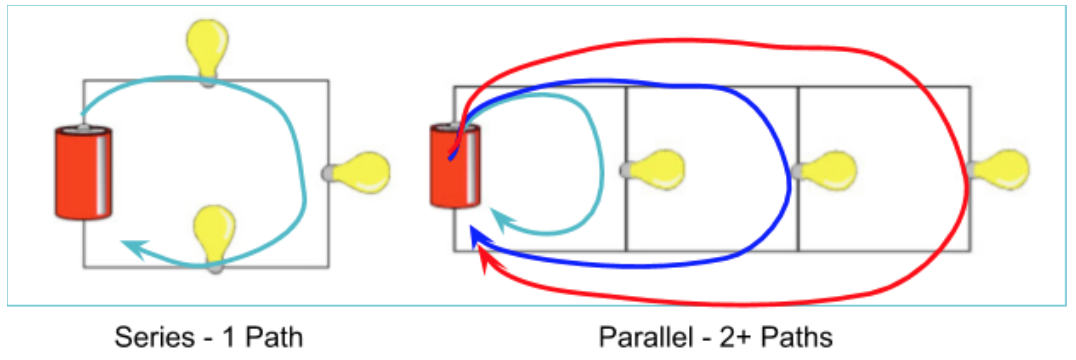
Circuit components can be connected in either Series or Parallel. A series connection, has 1 path between the components that all the current must travel through. A parallel circuit has 2 or more paths between the components. The current in a parallel circuit is split between all the available paths.
Electrical Current (I**)**
Current is the flow of electric charge through a conductor in an electric circuit. You can think of electrical current as being similar to the flow of water through a pipe, hose, or stream. The more water that passes a given point each second, the faster the current is. With electric current, the more charge that passes through a conductor each second, the more current there is. Mathematically, this can be represented by the following equation:

Where I is the current (measured in Amperes), q is the current traveling through the wire (measured in Coulombs), and t is the time for the current to travel through the wire.
Review: Remember in Unit 8, the charge is conserved. This means that throughout a given circuit, the total amount of charge must be kept the same. Charge CANNOT be “Used Up” in a circuit.
Other Key Circuit Terms 📍
Besides Current, there are two other commonly used terms for describing circuits. They are Voltage and Resistance. In addition, you’ll see the electrical energy and power mentioned occasionally as well.
Voltage
Voltage is the amount of energy each electron (or other charge carriers) is given as it travels through the circuit. The source of voltage for a circuit is usually a battery of some type. As the electrons travel throughout the circuit, they transfer their energy to the device (light bulb, motor, etc) and reduce their voltage accordingly. This is referred to as a voltage drop and will be important as we analyze circuits later in this unit.
Resistance
Resistance is the opposition to electrical current. It is often related to the characteristics of the conductor (more on this in 9.2). To use the water analogy, resistance is similar to a kink or twist in a hose. It reduces the flow of water outwards. With electrical circuits, resistors are added to the circuit to reduce the current to the desired value. Often these resistances convert the energy of the circuit into heat.
Mathematical Relationship (Ohm’s Law)
For an “ideal” resistor, the current, voltage and resistance can be calculated using the equation:
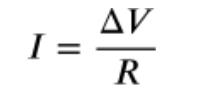
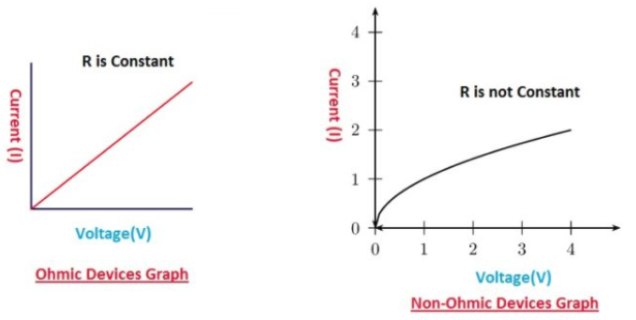
Graphically, this relationship is shown below.
Power
Electric Power is the rate at which electrical energy is used in a circuit. While the reference tables only show one equation to calculate power, you can use Ohm’s law to tweak the equation to use whatever terms you are given (V,I,R).
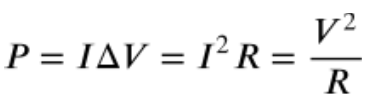
🎥Watch: AP Physics 1 - Unit 9 Streams

© 2024 Fiveable Inc. All rights reserved.