2.6 Linear Regression Models

What is a LSRL?

Linear regression is a statistical method used to model the linear relationship between a dependent variable (also known as the response variable) and one or more independent variables (also known as explanatory variables). The goal of linear regression is to find the line of best fit that describes the relationship between the dependent and independent variables. 🔍

The least squares regression line is a specific type of linear regression model that is used to minimize the sum of the squared differences between the observed values of the dependent variable and the predicted values of the dependent variable. This line is also known as the "line of best fit" because it is the line that best fits the data points on the scatterplot.

In simple linear regression, there is only one independent variable, and the line of best fit is a straight line that can be represented by the equation ŷ = a + bx, where ŷ is the predicted value of the dependent variable, x is the value of the independent variable, a is the y-intercept (the value of ŷ when x = 0), and b is the slope (the change in ŷ for a given change in x). 

Once we have calculated the slope and y-intercept, we can plug these values into the equation ŷ = a + bx to find the equation for the least squares regression line.

Again, it's important to recognize that our ŷ represents our predicted response variable value, while x represents our explanatory value variable. Since x is given in a data set, it is not necessarily predicted, but our y-value is always predicted from a least squares regression line.

Extrapolation

When you have a linear regression equation, you can use it to make predictions about the value of the response variable for a given value of the explanatory variable. This is called interpolation, and it is generally more accurate if you stay within the range of values of the explanatory variable that are present in the data set.

Extrapolation is the process of using a statistical model to make predictions about values of a response variable outside the range of the data. Extrapolation is generally less accurate than interpolation because it relies on assumptions about the shape of the relationship between the variables that may not hold true beyond the range of the data. The farther outside the range of the data you go, the less reliable the predictions are likely to be. 😔

It's important to be cautious when making extrapolations, as they can be prone to errors and can sometimes produce unrealistic or misleading results. It's always a good idea to be aware of the limitations of your model and to be mindful of the risks of extrapolation when making predictions based on your model.

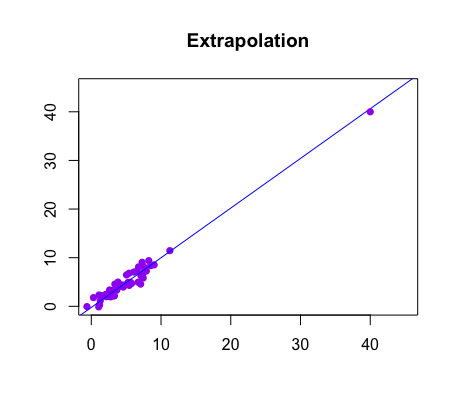
image courtesy of:  statsforstem.org comfort

Example

In a recent model built using data for 19-24 year olds, a least squares regression line is developed that says that an individual's comfort level with technology (on a scale of 1-10) can be predicted using the least squares regression line: ŷ=0.32x+0.67, where ŷ is the predicted comfort level and x represents one's age. 🚀 

Predict what the comfort level would be of a 45 year old and why this response does not make sense.

ŷ = 0.32 (45) + 0.67

ŷ= 15.07 comfort level

This answer does not make sense because we would expect our predicted comfort levels to be between 1 and 10. 15.07 does not make sense. The reason why we have this response is because we were using a data set intended for 19-24 year olds to make inference about a 45 year old. We were extrapolating our data to include someone outside our data set, which is not a good idea. 🙅‍♂️💡

Practice Problem

A study was conducted to examine the relationship between hours of study per week and final exam scores. A scatterplot was generated to visualize the results of the study for a sample of 25 students.

Based on the scatterplot, a least squares regression line was calculated to be ŷ = 42.3 - 0.5x, where ŷ is the predicted final exam score and x is the number of hours of study per week. 📖

Use this equation to predict the final exam score for a student who studies for 15 hours per week.

Answer

To solve the problem, we need to use the equation for the least squares regression line, which is ŷ = 42.3 - 0.5x, where ŷ is the predicted final exam score and x is the number of hours of study per week.

We are asked to predict the final exam score for a student who studies for 15 hours per week, so we can plug this value into the equation to calculate the predicted value of ŷ:

ŷ = 42.3 - 0.5 * 15

= 42.3 - 7.5

= 34.8

Interpretation in Context: Therefore, the predicted final exam score for a student who studies for 15 hours per week is 34.8

🎥 Watch: AP Stats - Least Squares Regression Lines