7.7 Justifying a Claim About the Difference of Two Means Based on a Confidence Interval

As you recall from Unit 7.3, a statistical claim is any belief that any population is equal (or not equal) to a given number or proportion. In dealing with two populations, our statistical claim is generally regarding whether these two populations are the same or different. Our null statistical claim when dealing with two different populations is that they are not different. In other words, their means are the same. 🐟

Making a Conclusion

When given a confidence interval and making a conclusion, there is a preset template that we can use that helps us to be sure to include all of the vocabulary necessary to score well on the AP Statistics exam. 📙

Template

Our template should go as follows:

• "We are % confident that the true difference in population means between _______ and _______ (context of problem) is (, ___).
• "In repeated random sampling with the same sample size, approximately C% of confidence intervals created will capture the difference of population means (add more about context). As with any AP Statistics Free Response question, it is always imperative that your answer includes context of the problem given. After all, a comprehensive interpretation for a confidence interval for the difference of two population means should include a reference to the samples taken and details about the populations they represent.

When testing for the difference in two populations, it is also important to use that interval to test the claim that the two populations are the same. If the two populations are statistically "the same," 0 will be included in your interval. If after completing your interval, you do not have 0 in your interval, there is reason to believe that your two populations do, in fact, have different means.

Finishing Our Apples to Apples Example

Let's finish our example with the green apples and red apples. 🍏🍎

In Unit 7.5, we concluded that our confidence interval for the difference in our two color apples was (0.408, 0.592). Our conclusion should go as follows:

"We are 95% confident that the true difference in the population means of the weights of green apples and red apples is between (0.408, 0.592). Since 0 is not included in our interval, we have significant evidence that the weights of green apples and red apples are in fact different."

Notice since 0 was not in our interval, that tells us, with 95% confidence, that there is some sort of difference in our two population means.

image courtesy of pixabay

Relating Confidence Intervals and Sample Sizes

When all other things remain the same, the width of the confidence interval for the difference of two means tends to decrease as the sample sizes increase**.** That's right: the width of the confidence interval for the difference of two means (also known as the margin of error) is inversely proportional to the sample size. 

Recall that the confidence interval represents the range of values within which the true population parameter is likely to fall, with a certain level of confidence. In the case of the difference of two means, the confidence interval is calculated by taking the difference between the two sample means and adding and subtracting the margin of error. The margin of error is calculated based on the standard error of the difference between the means and the desired level of confidence.

Increasing the sample size allows for a more precise estimate of the population parameter, which results in a narrower confidence interval and a smaller margin of error.

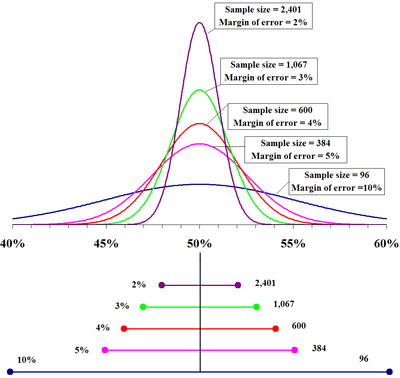
Source: Medium

🎥 Watch: AP Stats - Inference: Confidence Intervals for Means