<< Hide Menu
1.4 Polynomial Functions and Rates of Change
1 min read•june 18, 2024
1.4 Polynomial Functions and Rates of Change
🤓 A Refresher on Polynomial Functions
Wanna see what a polynomial function looks like? You’ve probably seen a lot of them throughout your math classes.
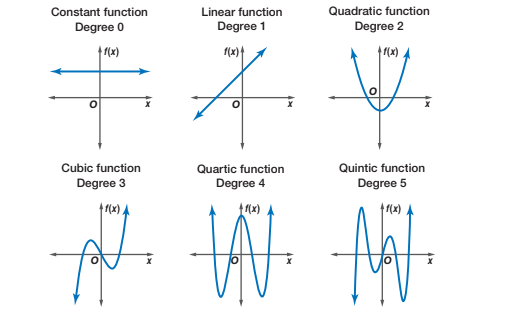
Image Courtesy of Wikiversity
Looks familiar, right? What do polynomial functions mean, though? 🤔
A polynomial function is a type of mathematical function that is represented by a sum of terms, where each term consists of a constant coefficient multiplied by a variable raised to a non-negative integer power.
A nonconstant polynomial function of x is one that is not a constant, and is represented by the general form , where is a positive integer, is a real number for each from 0 to , and is nonzero. The leading term is and the leading coefficient is .
A constant function is also considered a polynomial function of degree zero.
📊 Minima and Maxima
When analyzing the behavior of a polynomial function, it’s important to understand how it changes as the input variable increases or decreases. One key concept is the idea of a "switching point," where the function changes from increasing to decreasing or vice versa. At these points, the function will have a local maximum or minimum output value, which is the highest or lowest point on the function in the immediate vicinity of the switching point.
In some cases, the polynomial function may have a restricted domain, which means that it only applies within a certain range of input values. At the endpoint of this range, the function may also have a local maximum or minimum. These points are important because they represent the highest or lowest possible output values for the function within its domain.
When considering all of the local maxima or minima of a polynomial function, it is possible to identify the greatest or least of these values. These points are known as the global or absolute maximum and minimum, respectively, and they represent the highest and lowest points on the entire function, regardless of its domain or any other constraints. 🌐

Image Courtesy of Wikimedia Commons
Polynomial functions are mathematical functions that can be expressed as a sum of terms, each consisting of a variable raised to a non-negative integer power, multiplied by a coefficient. These functions are widely used in mathematics and science to model a variety of real-world phenomena.
🧐 Where Are The Zeros?
One important concept in the study of polynomial functions is the location of their zeros, which are the input values that make the function output zero. If a polynomial function has two distinct real zeros, then there must be at least one point between them where the function has a local maximum or local minimum. 0️⃣
This is because the function must change sign as it passes through each zero, and in order for this to happen, it must have a point of inflection where its direction changes from increasing to decreasing, or vice versa. This point of inflection is necessarily a local maximum or local minimum.
Here’s another way to define inflection points: when a polynomial function changes from being concave up to concave down, it means that the function is increasing at an increasing rate, and then begins to increase at a decreasing rate. This corresponds to a point of inflection where the rate of change of the function is at its maximum.
Similarly, when a polynomial function changes from being concave down to concave up, it means that the function is decreasing at a decreasing rate, and then begins to decrease at an increasing rate. This corresponds to a point of inflection where the rate of change of the function is at its minimum.
🔢 Even Degree Polynomials
Moreover, the behavior of polynomial functions of even degree is also of particular interest. Polynomial functions of even degree have an even number of turning points, which are the points where the function changes direction from increasing to decreasing or vice versa.
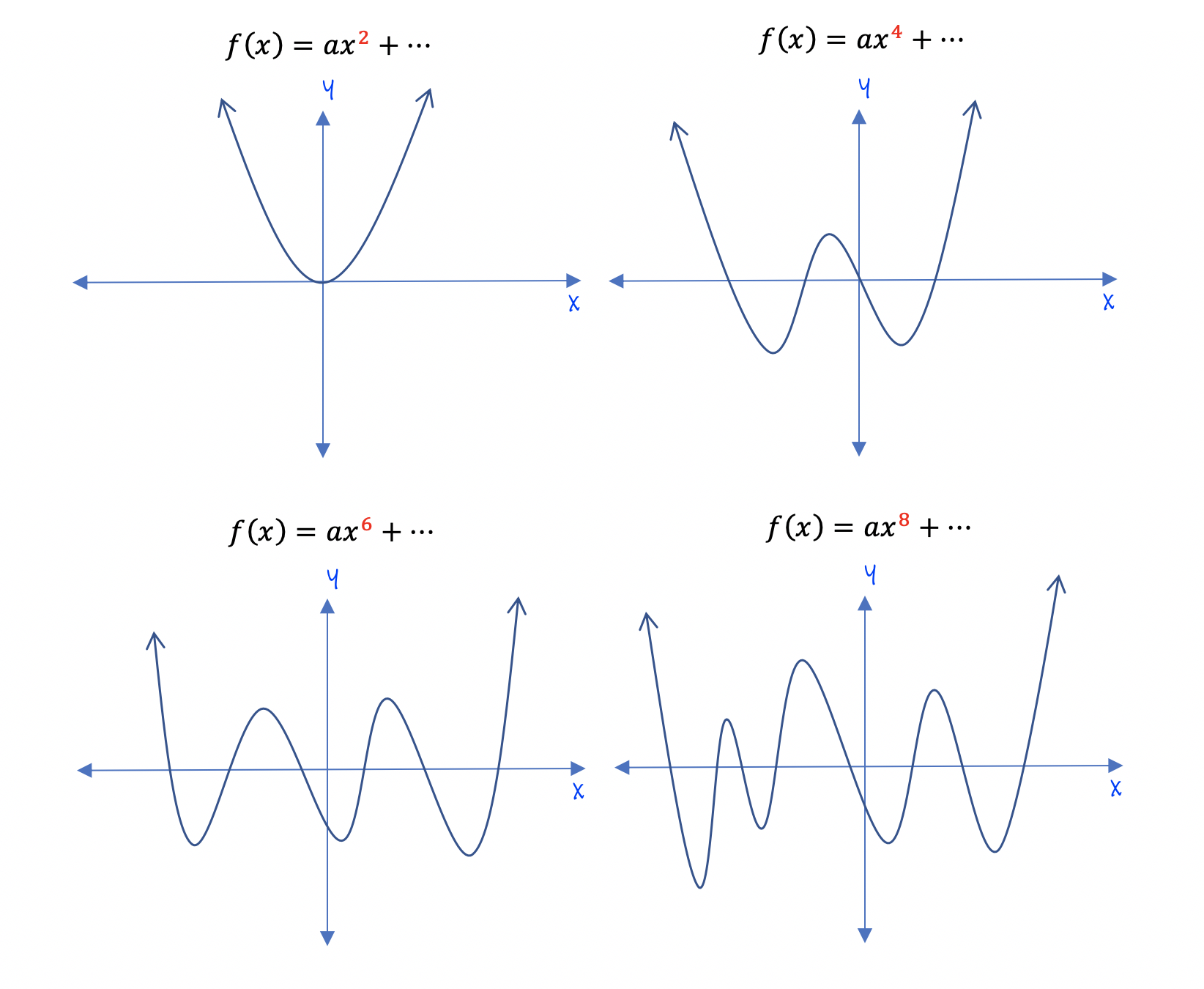
Image Courtesy of Jill Williams
Some trends to note:
- If the leading coefficient of an even degree polynomial is positive, the function will have a global minimum. 🔽
- If the leading coefficient is negative, the function will have a global maximum. 🔼
This is because the function will approach negative infinity as the input variable goes to either positive or negative infinity, and since it is continuous, it must reach a maximum or minimum point somewhere in between.

© 2024 Fiveable Inc. All rights reserved.