1.9 Rational Functions and Vertical Asymptotes

1.9 Rational Functions and Vertical Asymptotes

Connecting Multiplicities and Vertical Asymptotes

The presence of real zeros in the denominator of a rational function can have a significant impact on the behavior of the function. If a real number a is a zero of the polynomial function in the denominator, it means that the function becomes undefined at x = a. In particular, if a is not a real zero of the polynomial function in the numerator, then the function has a vertical asymptote at x = a.

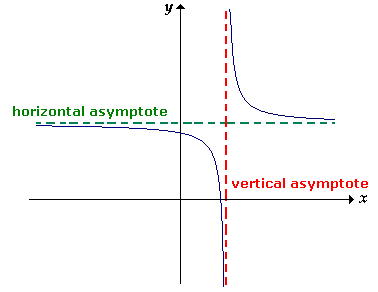
Image courtesy of Onlinemath4all

Furthermore, if the multiplicity of a as a real zero in the denominator is greater than its multiplicity as a real zero in the numerator, then the function approaches infinity or negative infinity as x approaches a. The multiplicity of a zero refers to the number of times it appears in the factorization of the polynomial.

For example, if a is a zero of multiplicity 3 in the denominator and multiplicity 1 in the numerator, then the function will approach infinity or negative infinity faster near x = a compared to the case when the multiplicities are equal.

It is important to note that the converse of this statement is not necessarily true. In other words, the presence of a vertical asymptote at x = a does not necessarily imply that a is a zero of the polynomial function in the denominator. There may be cases where the function has a vertical asymptote due to other reasons, such as a square root function appearing in the denominator.

For example, consider the rational function:

r(x) = (x + 1) / (x² - 1)

The polynomial function in the denominator has real zeros at x = -1 and x = 1. However, the polynomial function in the numerator has a real zero only at x = -1. Therefore, the function has a vertical asymptote at x = 1. We can confirm this by looking at the limits of the function as x approaches 1 from the left and right:

$\lim_{x\to 1^-}(x+1)/(x^2-1) = -\infin$

$\lim_{x\to 1^+}(x+1)/(x^2-1) = \infin$

As expected, the function approaches negative infinity as x approaches 1 from the left and approaches infinity as x approaches 1 from the right.

Image courtesy of SlidePlayer