2.7 Composition of Functions

2.7 Composition of Functions

Composite functions are functions made up of two or more simpler functions put together. Similarly, the process of combining functions is called composition of functions. 🧩

The basic notation for composite functions is f(g(x)), where f and g are two functions and x is the variable in the function. The first function, g(x), is applied to the variable x, and the result is then input into the second function, f(x). The output of the composite function is the final result of applying both functions, one after the other.

For example, if we have a function f(x) = x^2 and a function g(x) = 2x + 1, the composite function would be f(g(x)) = (x^2) = (2x + 1)^2, The function g(x) is applied first, so the x in g(x) is replaced by 2x+1 and the result is squared.

Source: Maths at Home

One of the key ideas when working with composite functions is that the output of the first function is used as the input of the second function. Therefore, by using the output values of g(x) as input values for f(x), we can calculate or estimate the values of the composite function f(g(x)).

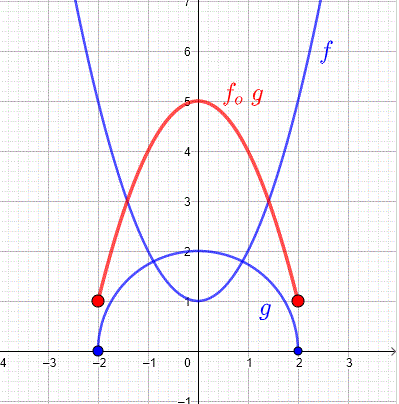
This method can also be applied to graphical representations of f and g by using the graph of g(x) to find the output values of g(x), and then using these values as input values for the graph of f(x), the corresponding output values for f(g(x)) can be found graphically. 📊 

📝 Notation and Properties

Composite functions can also be represented using function notation, where the output of the first function is the input to the second function, denoted as f(g(x)) = f(x) composed g(x) = f • g(x).

1️⃣ The order of the functions matters and can produce different results. Specifically, the composition of functions is not commutative, meaning that f(g(x)) and g(f(x)) are typically different functions [ f(g(x)) =/= g(f(x)) ].

For example, consider two functions f(x) = x^2 and g(x) = 2x + 1. The composite function f(g(x)) = (2x+1)^2, while the composite function g(f(x)) = 2x^2 + 1. These two composite functions are different and have different properties, and they could not be derived by simply changing the order of the functions.

2️⃣ Identity function: The identity function, f(x) = x, is a special function that when composed with any other function g(x), results in the same function g(x).

This means that g(f(x)) = f(g(x)) = g(x) for any function g(x). This property is similar to the properties of the additive identity 0 and the multiplicative identity 1 in arithmetic.

For example, consider the function g(x) = 2x + 1. If we compose the identity function f(x) = x with g(x), the resulting composite function is g(f(x)) = g(x) = 2x+1, which is the same function as g(x)! 🤯

This is because the identity function simply returns the input value as the output value, so when it is composed with another function, it does not change the original function. This is similar to how adding 0 to a number does not change its value, and multiplying a number by 1 does not change its value.

🧑🏿‍💻 Working with Composite Functions

It’s important to understand how to construct an analytic representation of f(g(x)), given analytic representations of f(x) and g(x). One method to achieve this is by substituting g(x) for every instance of x in f(x). This process is called function composition, and it is a way to create a new function from two existing functions.

Another way to construct a representation of f(g(x)) is by using numerical or graphical methods. For numerical methods, we can calculate or estimate values for (x, f(g(x))) by using a table of values for g(x) as input values for f(x) and calculating the corresponding output values for f(g(x)).

Similarly, for graphical methods, we can use the graph of g(x) to find the output values of g(x), and then use these values as input values for the graph of f(x) to find the corresponding output values for f(g(x)).

Source: Free Math Tutorials

🔨 Function Decomposition

Function decomposition, on the other hand, is particularly useful when working with functions that are given analytically, as it allows us to break down the function into simpler parts that are easier to understand and work with. 🧸

When decomposing a function, you need to ensure that the variable in one function replaces each instance of the function with which it was composed. This is known as the substitution property, and it is crucial to ensure that the function is properly decomposed.

For example, consider the function f(x) = (2x+1)^2. We can decompose this function by taking the square root of both sides of the equation, which gives us f(x) = √((2x+1)^2) = |2x+1|. The variable x replaces each instance of the function (2x+1) in the original function, which means that the function has been properly decomposed.

🦸🏽 Transformation Time!

We also often encounter transformations of functions that result in changes to the shape and position of the graph—and composite functions are not exempt from this idea! Two common types of transformations are additive and multiplicative. 💄

An additive transformation of a function, f(x), that results in a vertical translation of the graph can be understood as the composition of the function g(x) = x + k with f(x). This means that the graph of the transformed function is obtained by taking the graph of f(x) and shifting it upward or downward by a constant value k. The value of k represents the amount of the shift.

A multiplicative transformation of a function, f(x), that results in a horizontal dilation can be understood as the composition of the function g(x) = kx with f(x). This means that the graph of the transformed function is obtained by taking the graph of f(x) and stretching or shrinking it horizontally by a factor of k. The value of k represents the amount of the dilation.

When we apply these transformations, we can use the properties of the function g(x) to understand how the transformation affects the original function. 😁

For example, when we apply the function g(x) = x + k to f(x), we can see that the output of g(x) is the input of f(x) plus k, which means that the graph of f(x) is shifted vertically by k units. Similarly, when we apply the function g(x) = kx to f(x), we can see that the output of g(x) is the input of f(x) multiplied by k, which means that the graph of f(x) is dilated horizontally by a factor of k.