<< Hide Menu
2.14 Logarithmic Function Context and Data Modeling
1 min read•june 18, 2024
2.14 Logarithmic Function Context and Data Modeling
Feeling like a logarithmic master at this point? Lucky for you, we’ll finally move on to the ultimate way to apply what you’ve learned so far: data modeling in context!
Logarithmic functions are, in fact, used to model situations involving proportional growth or repeated multiplication. The logarithm of a number x is the exponent to which the base b must be raised to equal x. In other words, it represents the number of times b must be multiplied by itself to equal x! 🚴♂️
Because logarithmic functions are inverses of exponential functions, they can be used to model situations where the input values change proportionally over equal-length output-value intervals. For example, logarithmic functions can be used to model population growth, radioactive decay, and sound level. 📊
🎧 Sample Application: The Sound of Music
Sound level is often measured in decibels (dB), which are logarithmically related to the intensity of a sound. The intensity of a sound is measured in watts per square meter (), and the relationship between intensity and decibels is given by the equation: 🎵
where L is the sound level in decibels, I is the intensity of the sound, and is a reference intensity, typically taken to be the threshold of human hearing, which is approximately .
Let's say we want to model the sound level of a rock concert in a large stadium. We measure the sound intensity at various locations throughout the stadium and record the following data:
| Location | Intensity () |
| Stage | 1.0 |
| Front row | 0.1 |
| Middle of the crowd | 0.01 |
| Back of the crowd | 0.001 |
To find the sound level in decibels at each location, we can use the equation for sound level given above and plug in the measured intensity and reference intensity:
For the stage:
For the front row:
For the middle of the crowd:
For the back of the crowd:
We can see that the sound level decreases as we move away from the stage, with a difference of 10 dB between each location. This makes sense as we expect sound intensity to decrease as the distance from the source increases. 📈
Now, we can build a logarithmic function to model this relationship, we can use the formula , where y is the sound level, x is the intensity, m and c are constants
From the data we have the following points (x,y) (1,120), (0.1,110), (0.01,100), (0.001,90)
We can use these points to find out the value of m and c:
m=10
c=0
So the logarithmic function model is: .
We can use this function to predict the sound level at any intensity, such as 0.0001 W/m^2, we just need to plug in the value into the function:
This logarithmic function model can be used to predict the sound level at any intensity, and it gives us a way to quantify the relationship between sound intensity and sound level in decibels! 🤓
📉 Lines and Logarithmic Regression
A logarithmic function model can be constructed from an appropriate proportion and a real zero or from two input-output pairs. This can be done by finding the equation of the line of best fit and then transforming it into the logarithmic form. 👍
Technology, such as logarithmic regression, can be used to construct logarithmic function models for a data set. The natural log function, represented by the equation , is often useful in modeling natural phenomena, such as growth and decay.
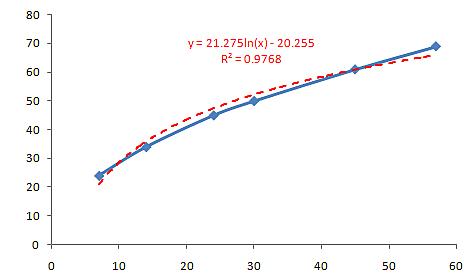
Image Courtesy of Micro PedSim
Logarithmic function models can also be used to predict values for the dependent variable, based on the characteristics of the context or data set. In addition, logarithmic functions are used in many areas such as physics, chemistry, engineering, economics, and business to model real-world phenomena. ⚛️

© 2024 Fiveable Inc. All rights reserved.