2.12 Logarithmic Function Manipulation

2.12 Logarithmic Function Manipulation

Fun fact: in precalculus, we can manipulate exponential functions in various ways to simplify them, to solve equations or to model real-world situations! Here, we’ll refer to each of them as a “property” to remember them more easily! 🎐

As we progress through this unit, we learned two things (among many others) about exponential functions:

1. Manipulating exponential functions in various ways allows us to simplify, solve, and or model them in various contextual scenarios
2. Exponential functions are inverses of the well-loved logarithmic functions; in other words, logarithmic functions "undo” exponential functions

Since we know (2) is true, then logarithmic functions follow the same principle conveyed in (1)! Like exponential functions, log functions are manipulable in different ways to serve different amazing purposes. Again, we’ll refer to each of these “manipulations” as properties. 🕰️

(If none of these ring a bell, check out section 2.4 Exponential Function Manipulation before proceeding!)

Properties of Logarithmic Functions

✖️ Product Property

The product property for logarithms states that the logarithm of the product of two numbers is equal to the sum of the logarithms of each of the numbers. In mathematical notation, this can be written as log_b(xy) = log_b(x) + log_b(y) where b is the base of the logarithm. ⛰️

Graphically, this property can be interpreted as a horizontal dilation of a logarithmic function, f(x) = log_b(kx), being equivalent to a vertical translation, f(x) = log_b(kx) = log_b(k) + log_b(x) = a + log_b(x), where a = log_b(k).

This means that if we were to stretch or compress the x-values of a logarithmic function horizontally, it would be equivalent to shifting the y-values of the function up or down. The horizontal dilation is represented by "k" and the vertical translation by "a."

Source: Statistics Lectures

For example, a logarithmic function f(x) = log_b(x) can be transformed to f(x) = log_b(2x) by multiplying x by 2. This will have the effect of stretching the graph horizontally by a factor of 2, which is the same as adding log_b(2) to the y-value of each point of the graph, which is a vertical translation!

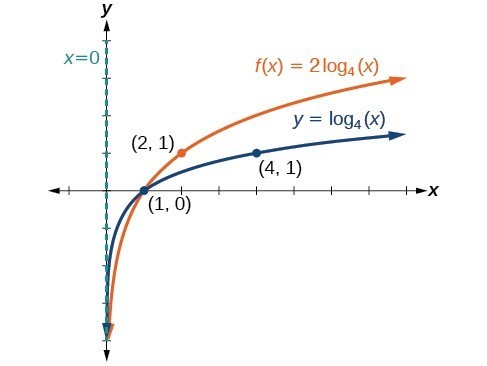
🦸🏽 Power Property

The power property of logarithms states that for any positive real numbers b, n, and x, log_b((x)^n) = nlog_b(x). 👊

This property can be understood by considering the relationship between logarithms and exponents. If we raise the base of a logarithm to a power, we are essentially multiplying the exponent by that power. Therefore, the property is a direct result of the definition of logarithms as exponents.

Graphically, this property implies that raising the input of a logarithmic function to a power, f(x) = log_b((x)^k), results in a vertical dilation of the graph of the function. This is because the input of the function is being raised to a power, which changes the scale of the x-axis. As a result, the graph of the function will be stretched or compressed along the y-axis.

The factor k in the function f(x) = log_b((x)^k) represents the constant of proportionality between the input and output of the function, and it determines the amount of dilation. For example, if k = 2, the graph of the function will be stretched vertically by a factor of 2, and if k = 0.5, the graph will be compressed vertically by a factor of 0.5.

Source: Statistics Lectures

For example, if we take log base 2 of 8, we know that log_2(8) = 3, because 2^3 = 8. Using the power property, we can also write this as log_2(2^3) = 3 * log_2(2) , which confirms that the logarithm of a power is equal to the exponent times the logarithm of the base.

This property is also useful in solving equations with logarithms. For example, if we have an equation like log_3(x^2) = 2, we can use the power property to change it to 2 * log_3(x) = 2, and then solve for x.

Source: Lumen Learning

This is consistent with the previous property: the logarithm of a product is the sum of the logarithms of the factors, but only for the same base, for example log_2(4x) = log_2(4) + log_2(x)

🔄 Change of Base Property

The change of base property for logarithms is a useful tool for simplifying and manipulating logarithmic equations. It states that for any two bases, a and b (where a > 0 and a ≠ 1), the logarithm of a number x with respect to base a is equal to the logarithm of x with respect to base b divided by the logarithm of b with respect to base a. 🏷️

In other words, log_b(x) = log_a(x) / log_a(b)

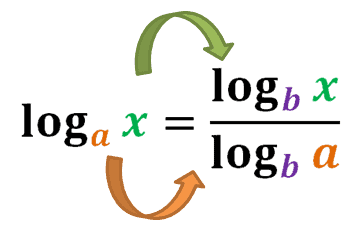
Source: The Story of Mathematics

This relationship can be understood in terms of the graph of the logarithmic functions. The graph of a logarithmic function with a given base is a reflection of the graph of the same function with a different base across the line y = x. This means that all logarithmic functions are similar, and the change of base formula shows how to convert from one base to another.

Furthermore, all logarithmic functions are vertical dilations of each other. The height of the graph of a logarithmic function with a given base is inversely proportional to the logarithm of the base. This means that a logarithmic function with a smaller base will have a taller graph, while a logarithmic function with a larger base will have a flatter graph. 🗼

Natural Logs and e

The natural logarithm, denoted by ln(x), is the logarithm of x to the base e, where e is the mathematical constant approximately equal to 2.71828. The function f(x) = ln(x) is a logarithmic function with the natural base e. This means that the value of the function at x is the exponent to which e must be raised to equal x. In other words, ln(x) = log_e(x) is the inverse function of e^x.

The natural logarithm, while seemingly random at first, actually has many useful properties and applications in mathematics and science. For example, it is commonly used in calculus to solve problems involving exponential growth and decay. It is also used in physics and engineering to solve problems involving rates of change, such as radioactive decay and electrical circuit analysis. 🔦

Source: Online Math Learning

The natural log function is defined for all positive numbers. In other words, the domain of this function is all positive real numbers and range is all real numbers. 🥣