2.11 Logarithmic Functions

2.11 Logarithmic Functions

Now that we (hopefully) convinced you that logarithmic functions are not random functions that spawned in thin air…and are actually connected to our handy, dandy exponential function friends, we can now talk about the key characteristics of log functions! 😉

The Domain of a Function

The domain of a logarithmic function in general form, which is written as $y = log_b(x)$, is any real number greater than zero (x > 0). This is because the logarithm of a negative number or zero is undefined. The range of a logarithmic function is all real numbers. ⛩️

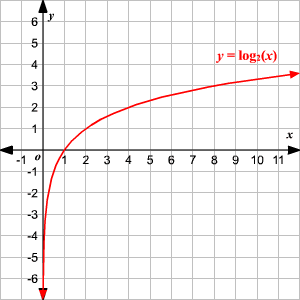
Image Courtesy of Varsity Tutors

Extrema, Concavity, and Inflection Points

Because logarithmic functions are inverses of exponential functions, the properties of logarithmic functions are closely related to the properties of exponential functions.

Specifically, if an exponential function is increasing, its inverse logarithmic function is also increasing, and if an exponential function is decreasing, its inverse logarithmic function is also decreasing. This means that the graph of a logarithmic function is always increasing or always decreasing, but never does both. 📈

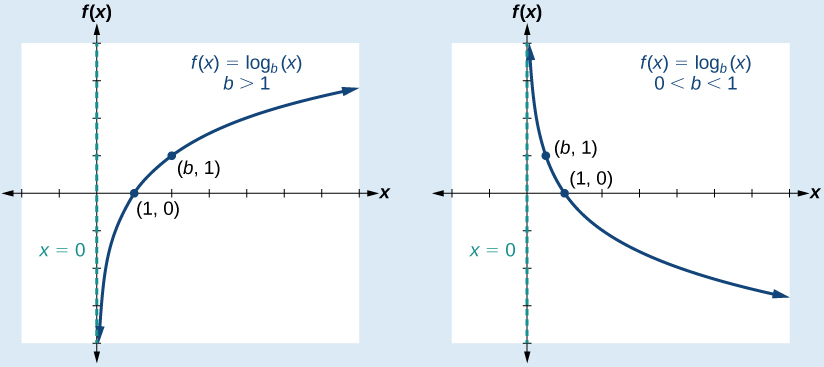
Image Courtesy of Phil Schatz

The graph of a logarithmic function is also always concave up or always concave down, depending on whether the logarithm is base-b or base-1/b. 🫡

Consequently, logarithmic functions do not have extrema except on a closed interval, and their graphs do not have inflection points. This is because logarithmic functions are always increasing or decreasing, and their graphs are always concave up or concave down, without any change in direction. 🪂

Image Courtesy of Lumen Learning

➕ Additive Transformation Function g(x) = f(x + k)

The additive transformation function, $g(x) = f(x + k)$, is a way to change the position of the graph of a function f by shifting it horizontally by a fixed amount k. In the case of a logarithmic function, f(x) = log(base b)x, the additive transformation function is $g(x) = log_b(x + k)$. ➕

When the input values of the additive transformation function, $g(x) = f(x + k)$, of a logarithmic function f are not proportional over equal-length output-value intervals, it means that the function g is not logarithmic. ❌ This is because the logarithmic function has the property that the input values are proportional over equal-length output-value intervals.

However, if the output values of the additive transformation function, $g(x) = f(x + k)$, of any function f are proportional over equal-length input-value intervals, then f is logarithmic. This is because the property that the output values are proportional over equal-length input-value intervals is a defining characteristic of logarithmic functions. ✅

In other words, if the graph of a function is such that the distance between two points on the graph is the same no matter where they are on the graph, then the function is logarithmic. The additive transformation function $g(x) = f(x+k)$ doesn't change the property of logarithmic function and thus it is still a logarithmic function.

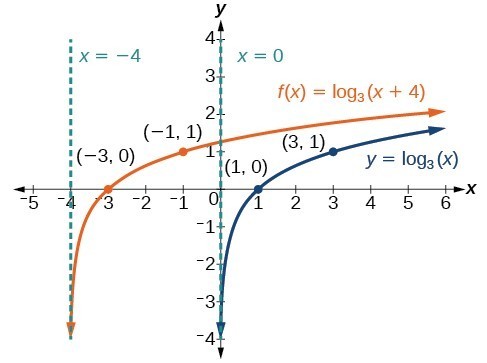
Image Courtesy of Lumen Learning

🛑 Limits and Asymptotes

With their limited domain, logarithmic functions in general form are vertically asymptotic to x = 0, meaning that as the input value, x, approaches zero, the function value, y, approaches positive or negative infinity (notice where the arrows are pointing when you draw log functions?). This is because the logarithm of a very small number is a very large negative number, and the logarithm of a very large number is a very large positive number.

The end behavior of a logarithmic function is unbounded, meaning that as x approaches either positive or negative infinity, y also approaches positive or negative infinity. ⛓️

• The limit of the logarithmic function $alog_b(x)$ as x approaches zero **from the right is +/- ∞ (positive or negative infinity)

• The limit of the logarithmic function $alog_b(x$) as x approaches infinity is also +/- ∞ (positive or negative infinity).

  

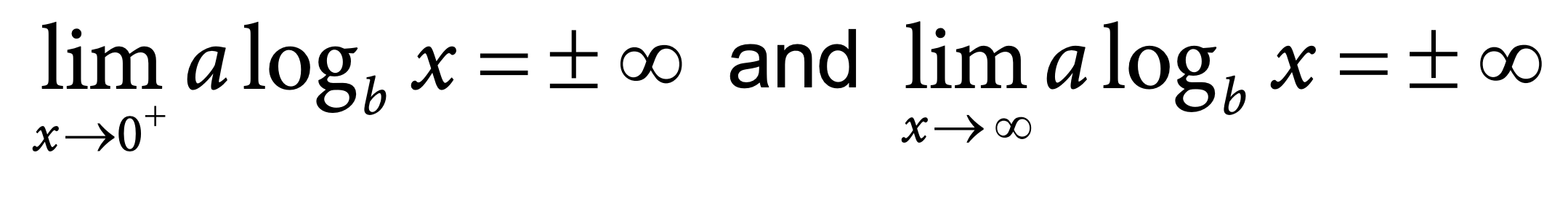
  Source: Jed Q