Unit 2 Overview: Exponential and Logarithmic Functions

2.0 Unit 2 Overview: Exponential and Logarithmic Functions

Unit 2 of AP Precalculus is focused on the study of exponential and logarithmic functions.

• Exponential functions are functions in the form of f(x) = ab^x where a and b are constants and b is greater than 0 and not equal to 1. These functions are used to model situations where the rate of change is proportional to the current value of the function.
• Logarithmic functions, on the other hand, are the inverse of exponential functions, and are written in the form of f(x) = log_b(x) where b is the base of the logarithm. Logarithmic functions are used to model situations where the rate of change is inversely proportional to the current value of the function.

In this unit, you will learn how to graph and analyze exponential and logarithmic functions, including the properties of asymptotes, domain and range, inverse functions and how to use these functions to model real-world situations. 🤯

Additionally, you’ll also learn how to solve exponential and logarithmic equations and how to use the properties of logarithms to simplify and manipulate logarithmic expressions.

One more thing you’ll learn is how to use semi-log plots, which is a powerful tool for visualizing and analyzing data or functions that have exponential characteristics. By using semi-log plots, students will be able to detect exponential growth or decay patterns in data without the need to add a constant to the dependent variable values and it allows for the fitting of exponential model to the data by finding the slope of the line on the semi-log plot.

🔨 Unit Breakdown

🔷 Arithmetic & Geometric Sequences

Arithmetic and geometric sequences are both types of mathematical sequences, but they have different characteristics. 💎

An arithmetic sequence is a sequence of numbers where the difference between any two consecutive terms is always the same. This common difference is usually represented by the variable "d." For example, the sequence 1, 3, 5, 7, 9 is an arithmetic sequence with a common difference of 2. The formula for an arithmetic sequence is un = a + (n-1)d, where a is the first term and d is the common difference.

On the other hand, a geometric sequence is a sequence of numbers where the quotient between any two consecutive terms is always the same. This common ratio is usually represented by the variable "r". For example, the sequence 2, 6, 18, 54 is a geometric sequence with a common ratio of 3. The formula for a geometric sequence is un = ar^(n-1) where a is the first term and r is the common ratio.

Source: ThingLink

↪️ Exponential & Logarithmic Functions

Exponential functions are mathematical functions of the form f(x) = ab^x where a and b are constants and b is greater than 0 and not equal to 1. These functions are used to model situations where the rate of change is proportional to the current value of the function. The graph of an exponential function is a curve that starts at the origin, and as x increases, the y-value increases at an increasing rate. 🐰

Exponential functions can be used to model a wide variety of real-world situations, such as population growth, radioactive decay, and compound interest.

Logarithmic functions, on the other hand, are the inverse of exponential functions and are written in the form of f(x) = log_b(x) where b is the base of the logarithm. Logarithmic functions are used to model situations where the rate of change is inversely proportional to the current value of the function. The graph of a logarithmic function is a curve that asymptotically approaches the x-axis as x increases. ⬆️

Logarithmic functions have many applications in science and engineering, such as in measuring sound intensity, pH levels and earthquake magnitudes.🧑🏽‍🔬

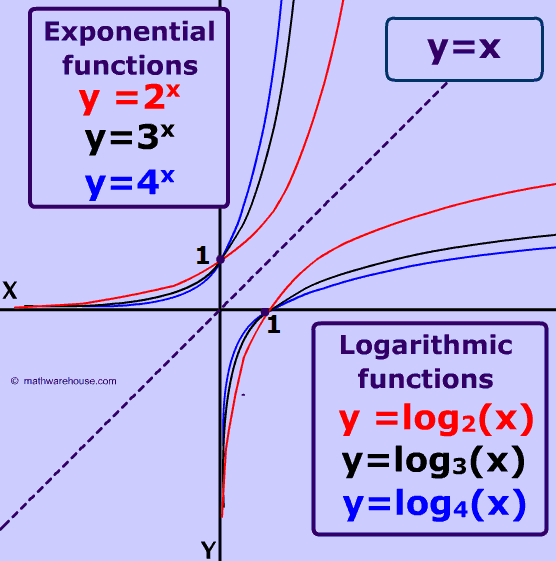
Source: Math Warehouse

⭕️ Composite Functions

Composite functions are functions made up of two or more functions combined together. The output of one function is used as the input for the other function. The order of the functions is important and can be denoted as (f o g)(x) = f(g(x)) where f is the outer function and g is the inner function. The composite function can also be represented using the notation f(g(x)). ✌️

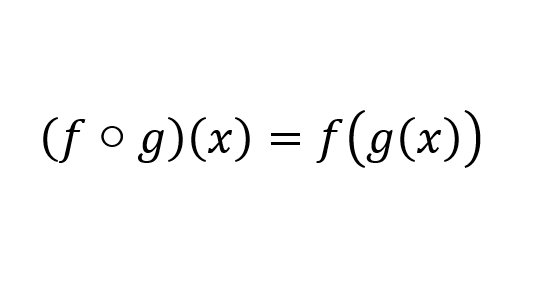
Source: Medium

🔄 Inverse Functions

Inverse functions are two functions that "undo" each other. For a function f(x), its inverse function is denoted as f^-1(x) and is defined as f(f^-1(x)) = x and f^-1(f(x)) = x. The inverse function can be found by swapping the x and y values of the original function and then solving for y. 🙃

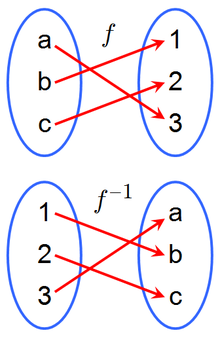
Source: Wikimedia Commons

🪵 Semi-log Plots

Semi-log plots are a type of graph that uses a logarithmic scale on one axis and a linear scale on the other axis. This type of plot is useful for displaying data or functions that have a wide range of values, as it allows for a better visual representation of the data. 🌞

When the y-axis of a semi-log plot is logarithmically scaled, data or functions that demonstrate exponential characteristics will appear linear. This allows for the detection of exponential growth or decay patterns in data without the need to add a constant to the dependent variable values, and it allows for the fitting of exponential model to the data by finding the slope of the line on the semi-log plot.

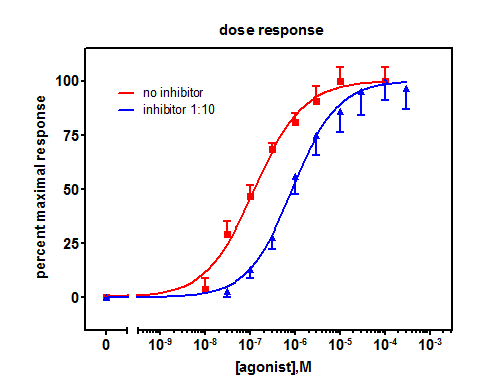
Source: GraphPad

This type of plot is particularly useful in fields such as biology, chemistry, physics, and electrical circuits, where data such as bacterial growth, reaction kinetics, radioactive decay, and circuit components vary over multiple orders of magnitude. In addition, semi-log plots are also used in the stock market to analyze stock prices and other financial data. ☢️