<< Hide Menu
Kashvi Panjolia
Kashvi Panjolia
Now that you have learned how to construct the sine and cosine graphs, you will analyze the behavior of these graphs more closely, then generalize the behaviors to apply to all the functions that look like a sine (or cosine) function. This topic is vocabulary-heavy, so make sure you comprehend the new vocabulary that is introduced.
Transformations of the Sine Curve
A sinusoidal function is a fancy name for any function that looks like the sine curve. Sine and cosine are both sinusoidal functions because their graphs are oscillating and periodic. Transformations of the sine and cosine functions are also called sinusoidal functions. In fact, the cosine function can actually be described as a transformation of the sine function by using the equation:
cosθ = sin(θ + 𝛑/2)
The sine function is moved to the left 𝛑/2 units to arrive at the cosine function. Remember from algebra that a number added or subtracted inside the parentheses of a function indicates a horizontal transformation of the function in the form of (x-h). Here, x is θ and h is 𝛑/2, so we are actually subtracting a negative 𝛑/2 to shift the function left to arrive at the cosine curve.
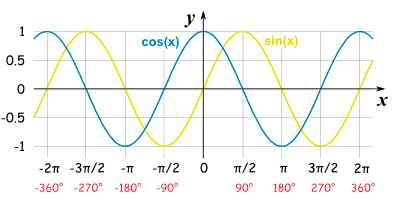
Image courtesy of Medium.
Characteristics of Sinusoidal Functions
All sinusoidal functions share some common characteristics. All sinusoidal functions have a period of oscillation, a frequency, an amplitude, and a midline. The functions also oscillate between concave down and concave up, and some functions have symmetry. A breakdown of what each term means is presented below:
-
Period: The period of a sinusoidal function is the length of one complete oscillation of the function. For a sine or cosine function, the period is 2𝛑 units along the x-axis. It is represented by the letter T. The period does not always have to be 2𝛑, however. The period is calculated by finding the distance between any starting point on a sinusoidal curve and the next time the graph arrives at that same y-value from the same direction. You can start measuring the period at the maximum value of the graph, the middle of the graph, the bottom, or any point in between, and it will yield the same period.
-
Frequency: The frequency of a sinusoidal function is the number of oscillations that occur in one unit of time. It is represented by the letter f, and is the reciprocal of the period for any graph. The frequency of the sine and cosine curves is 1/(2𝛑), and the frequency of any sinusoidal function is 1/period.
-
Midline: The midline of a sinusoidal function is the average value of the function over one period. It is the horizontal line that the function oscillates about, and is represented by the letter k. In simpler terms, the midline is the line that passes through the center of the wave, and can be calculated by finding the average between the y-values of the minimum and maximum of the function. For the sine and cosine curves, the midline is the line y=0.
-
Amplitude: The amplitude of a sinusoidal function is the vertical distance from the midline of the function to the maximum y-value of the function. The amplitude is always a positive value. The amplitude of the sine and cosine functions is 1, since the midline of the functions is at y=0 and the maximum value is y=1.
-
Odd symmetry: A sinusoidal function has odd symmetry if it is symmetric about the origin. This means that for every point on the graph (x, y), there is another point (-x, -y) that is the same distance from the origin but on the opposite side. Another way to think about odd symmetry is to visualize the function rotating 180 degrees about the origin. If it looks the same as the original function, then it has odd symmetry. To mathematically check if a function has odd symmetry, plug in -x into every x in the function. Then, multiply the original function by -1. If f(-x) = -f(x), then the function has odd symmetry. The sine function has odd symmetry.
-
Even symmetry: A sinusoidal function has even symmetry if it is symmetric about the y-axis. This means that for every point on the graph (x, y), there is another point (-x, y) that is the same distance from the y-axis but on the opposite side of the x-axis. You can also visualize this type of symmetry by reflecting the graph of the function over the y-axis. If the graph looks the same, the function is symmetrical with respect to the y-axis. To mathematically check if a function has odd symmetry, plug in -x into every x in the function, then compare it to the original function. If f(-x) = f(x), then the function has even symmetry. The cosine function has even symmetry.
-
Oscillation: A key component of sinusoidal functions is their oscillating behavior, meaning the function is ping-ponging between two values. The parts where a sinusoidal function is curved up (like a smile) are called the concave up portions of the graph, and the parts where a sinusoidal function is curved down (like a frown) are called the concave down portions of the graph. A sinusoidal function oscillates between concave up and concave down as the input values (x-values) increase.
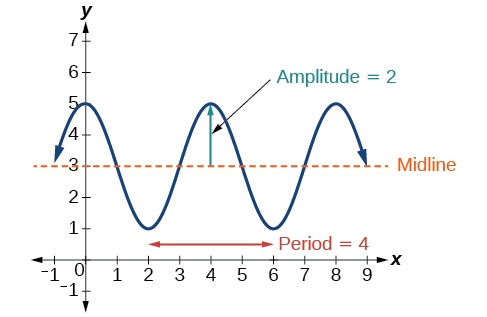
Image courtesy of MathLibreTexts.
For the graph above, the concave up sections are from x=1 to x=3 and x=5 to x=7. The concave down portions are from x=-1 to x=1, x=3 to x=5, and x=7 to x=9. This is a graph of the cosine curve shifted up four units. You can see how transformations of sine and cosine functions are still considered sinusoidal functions because this graph still has the general shape of a sine curve.
Practice Problems
1. Identify the amplitude and period of this function.

Image courtesy of MathIsFun.
b) Amplitude = 3; Period = 𝛑/2
c) Amplitude = 4; Period = 𝛑/4
Answer: d
2. Identify the frequency of the function below.
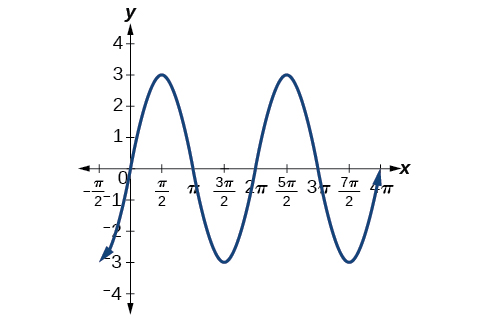
Image courtesy of CourseHero.
a) 𝛑
b) 1/𝛑
c) 2𝛑
d) 1/(2𝛑)
Answer: d
3. Identify the midline of the following function.
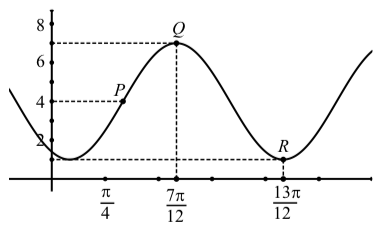
Image courtesy of MathLibreTexts.
a) x = 𝛑/4
b) y= 𝛑/4
c) x = 4
d) y = 4
Answer: d

© 2024 Fiveable Inc. All rights reserved.