<< Hide Menu
Jesse
Jesse
4.6 Conic Sections
Conic sections are geometric shapes that are created by the intersection of a plane and a cone. There are four types of conic sections: circles, ellipses, parabolas, and hyperbolas. Each type of conic section can be defined by a specific equation and has its own unique properties. 🍦
💡 Fun fact: The name "conic section" comes from the Latin word "conus," which means cone. The five types of conic sections are the circle, ellipse, hyperbola, and parabola.
- 🔵 A circle is created when the plane is parallel to the base of the cone and intersects the cone at the same point as the vertex.
- 🥚 An ellipse is created when the plane is inclined to the base of the cone, and the intersection forms a closed curve.
- ↪️ A parabola is created when the plane is parallel to one of the generators of the cone, and the intersection forms a U-shaped curve.
- 🔁 A hyperbola is created when the plane is inclined to the generators of the cone, and the intersection forms two disconnected curves.
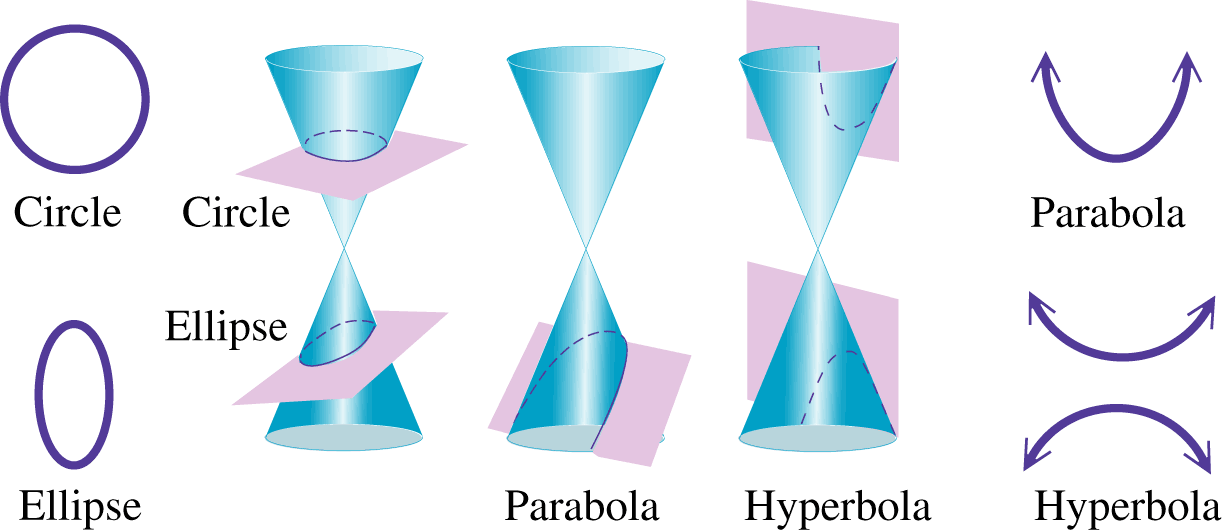
Source: A Plus Topper
Conic sections are important in mathematics and have many applications in science, engineering, and technology. 🧑🎓
In mathematics, conic sections are used to study algebraic equations, geometry, and trigonometry. In physics, conic sections are used to study the motion of planets and other celestial bodies, and in engineering, they are used to design equipment such as telescopes, satellite dishes, and radar systems. They are also used in the field of optics, where it is used to design lenses and mirrors for cameras, telescopes, and other optical instruments.
↪️ Parabola
The parabola is a specific type of conic section that is defined as the set of all points that are equidistant from a fixed point (called the focus) and a fixed line (called the directrix). The vertex of a parabola is the point at which the parabola reaches its highest or lowest point, depending on the orientation of the parabola. 🧐
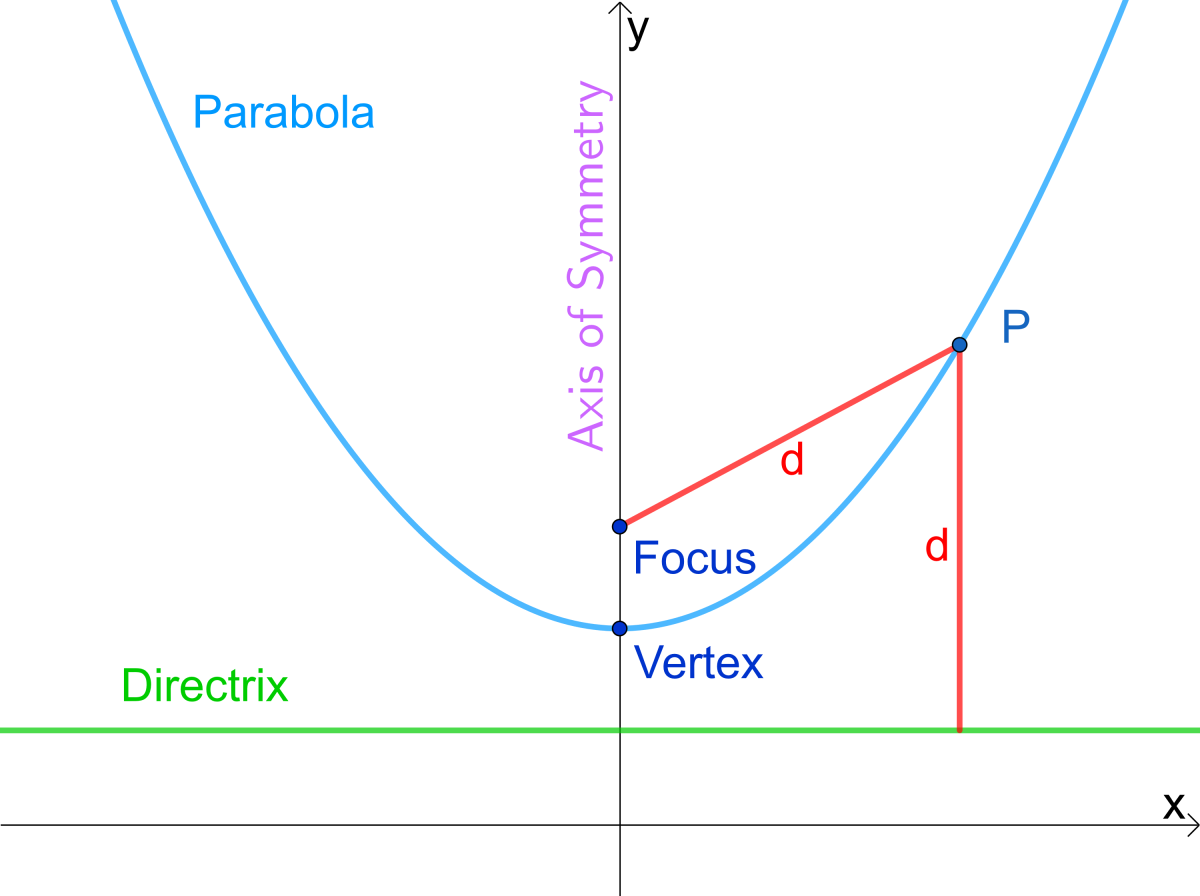
Source: Owlcation
The standard form of the equation of a parabola with vertex (h, k) that opens left or right can be represented as (y−k)^2 = a(x−h), where a is a non-zero constant. This equation can be derived by using the distance formula to find the distance between a point on the parabola and the focus and the directrix. If the parabola opens up or down, the equation can be represented as a(y− k) = (x−h)^2.
Parabolas have many applications in areas such as physics, engineering, and astronomy. In physics, parabolic reflectors are used to focus light or sound waves. In engineering, parabolic shapes are used in the design of antennas and other devices. In astronomy, parabolic mirrors are used in telescopes to reflect and focus light from distant objects. 🪞
Ellipse (and Circle)
An ellipse is a conic section that is created when a plane intersects a cone at an angle that is not parallel to the base of the cone. The shape of the ellipse is determined by the angle of the plane and the shape of the cone. It is defined by the property that the sum of the distances from any point on the ellipse to the two foci is constant. 🧠
The equation of an ellipse centered at the point (h, k) with horizontal radius a and vertical radius b is (x - h)^2 / a^2 + (y - k)^2 / b^2 = 1.
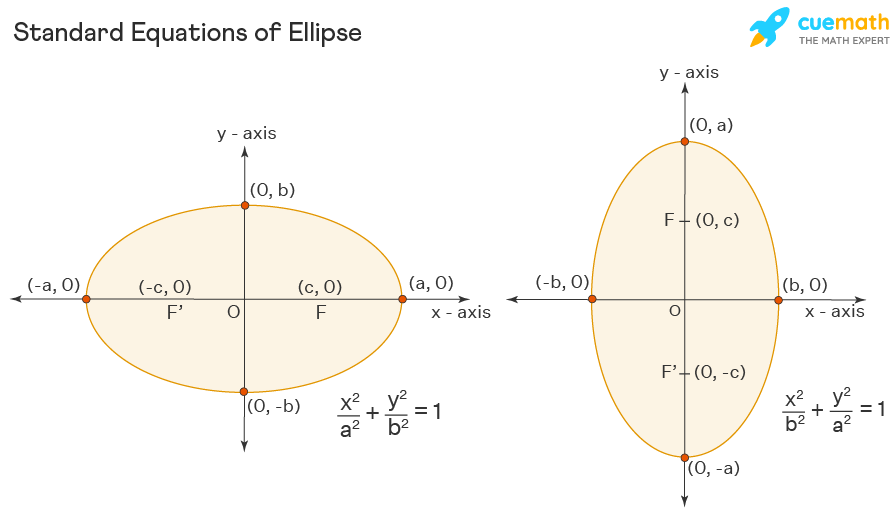
Source: Cue Math
An important concept related to the ellipse is the foci, which are two points on the major axis that are equidistant from the center and are the origin of the ellipse's unique properties. The distance between the center and a focus is called the "focal length" and is represented by the variable c. The relationship between a, b, and c is that c^2 = a^2 - b^2. 🤔
Ellipses have many real-world applications, including:
- In engineering, ellipses are used to design the cross-sections of many structures such as bridges, buildings and aircraft wings.
- In physics, ellipses are used to describe the orbits of planets and other celestial bodies.
- In image processing, ellipses are used to detect and track objects in images.
- In statistics, ellipses are used to represent confidence intervals in two-dimensional data.
A circle is a special case of an ellipse where a = b, and the equation of a circle is (x-h)^2 + (y-k)^2 = r^2, where (h, k) is the center of the circle and r is the radius.
🔁 Hyperbola
The hyperbola is a curve that is defined by the equation (x − h)^2 / a^2 - (y − k)^2 / b^2 = 1 for a hyperbola opening left and right, or as -(x − h)^2 / a^2 + (y − k)^2 / b^2 for a hyperbola opening up and down.
📝 Practice Problems
- What type of conic section is represented by the equation (x - 2)^2 - (y + 3)^2 = 1? a) Circle b) Ellipse c) Parabola d) Hyperbola
- What type of conic section is represented by the equation (x - 4)^2 / 9 + (y + 2)^2 / 4 = 1? a) Circle b) Ellipse c) Parabola d) Hyperbola
Answers
#1 d) Hyperbola
Explanation: The equation is in the standard form of a hyperbola, where the difference of the squared terms on either side of the equation is equal to 1. The center of the hyperbola is (2, -3) and the vertical and horizontal lines of symmetry, also known as the asymptotes, are parallel to the x and y axes respectively. ✌️
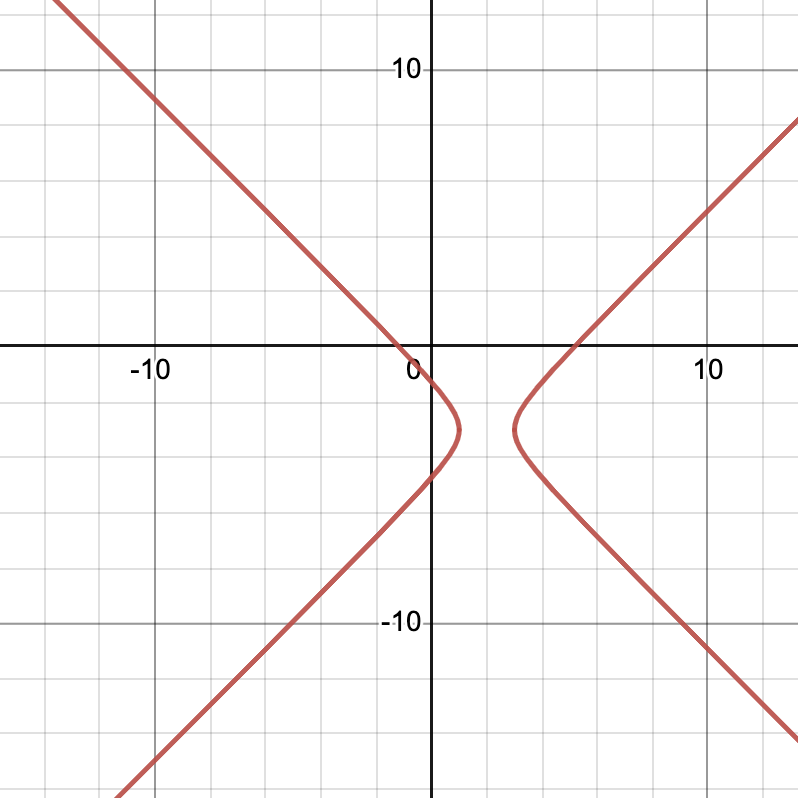
Source: Desmos
#2 b) Ellipse
Explanation: The equation is in the standard form of an ellipse, where the sum of the squared terms on either side of the equation is equal to 1. The center of the ellipse is (4, -2) and the vertical and horizontal radii are 4 and 3 respectively. The shape of the ellipse is elongated horizontally as the horizontal radius is larger than the vertical radius. 🤞
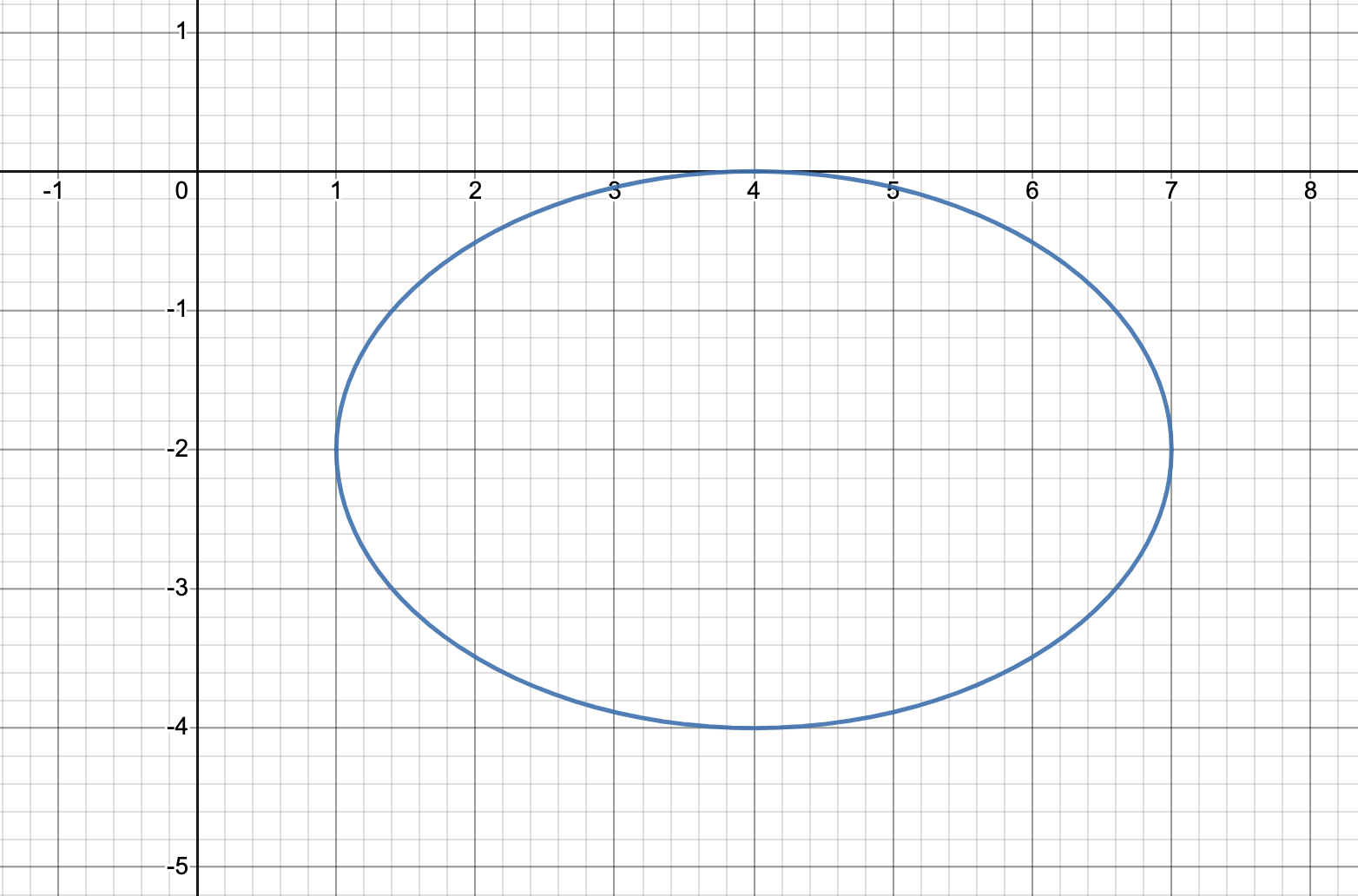
Source: Desmos

© 2024 Fiveable Inc. All rights reserved.