4.11 The Inverse and Determinant of a Matrix

4.11 The Inverse and Determinant of a Matrix

🤸 More Fun with Matrices

🫵 Identity Matrix and Inverses

The identity matrix, denoted as I, is a special type of square matrix that has the property that when it is multiplied by any other matrix of the same size, the resulting matrix is equal to the original matrix. Amazing, right? 🤯

The identity matrix has the size of n x n, where n is the number of rows and columns. The identity matrix has ones on the diagonal from the top left to bottom right, and zeros everywhere else. This diagonal of ones is often referred to as the main diagonal. ↗️ The identity matrix is also known as the unit matrix. 1️⃣

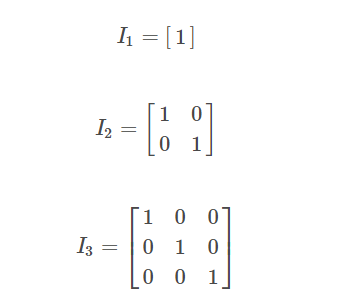
Source: Level Up Coding

The product of a square matrix and its inverse, when it exists, is the identity matrix of the same size. This means that if A is a square matrix and A^-1 is the inverse of A, then A * A^-1 = A^-1 * A = I, where I is the identity matrix of the same size as A. 😁

One way to calculate the inverse of a 2 x 2 matrix is to use the formula:

A^-1 = 1/det(A) * [a11, -a12; -a21, a22], where A = [a11, a12; a21, a22] is the original matrix, and det(A) is the determinant of A.

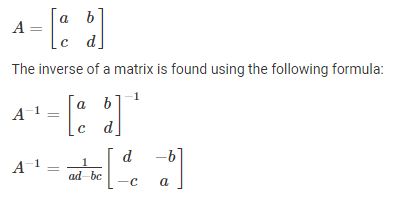
Source: Byjus

👊 Determinants

The determinant of a matrix is a scalar value that can be calculated for square matrices, and it is denoted as det(A). The determinant of a matrix A is a measure of its invertibility and it can be used to find the inverse of a matrix, when it exists. 🟩

The determinant of a matrix can also be calculated using technology such as a calculator or computer software. For example, a calculator with matrix capabilities can perform the calculation of the determinant of a 2 x 2 matrix, or a computer software like MATLAB or Python can be used to perform the calculation. 🖥

Let’s say we’re working on a 3 x 3 matrix “B” instead. How do we find the determinant for B (aka, what’s det(B)?)

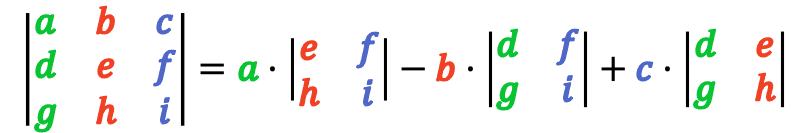
Source: Algebra Practice Problems

🙌 Relating Determinants and Parallel Vectors

if a 2 x 2 matrix A = [v1 v2] consists of two column vectors v1 and v2 from R2, then the nonzero absolute value of the determinant of the matrix is the area of the parallelogram spanned by the vectors represented in the columns of the matrix. ✈️

The determinant of the matrix A is given by **det(A) = |v1||v2|sin(θ) where θ is the angle between v1 and v2. The absolute value of the determinant is equal to the area of the parallelogram spanned by v1 and v2. This is because the area of the parallelogram is given by the base times the height and the base and height are given by the vectors v1 and v2 respectively. 💎

If the determinant of the matrix A equals zero, then the vectors are parallel. ⏸ This means that the angle between the vectors is either 0 or 180 degrees, meaning that the vectors are either pointing in the same direction or opposite directions. In this case, the area of the parallelogram is zero, and this is why the determinant is also zero. 0️⃣

It's worth noting that the same holds true for a 2 x 2 matrix A = [v1; v2], if the matrix consists of two row vectors v1 and v2 from R2. The determinant of the matrix A is still given by det(A) = |v1|*|v2|*sin(θ) where θ is the angle between v1 and v2, and if the determinant equals zero, then the vectors are parallel. 🤓

☝️ Invertibility Condition

The square matrix A has an inverse if and only if its determinant, denoted as det(A), is not equal to 0 [det(A) =/= 0]. This means that a square matrix A is invertible if and only if its determinant is non-zero. This is often referred to as the invertibility condition of a matrix. 🙃

Fun fact, aka no need to know for the exam: When the determinant of a matrix is not equal to zero, it means that the matrix is full-rank, meaning that its columns are linearly independent and span the entire space. This implies that it has a unique inverse. On the other hand, if the determinant of a matrix is equal to zero, it means that the matrix is not full-rank and it is called a singular matrix, it does not have an inverse. 🤔